Work Energy and Power Numerical
Question 1: 👇
A particle of mass approaches a region of force starting from r = +∞. The potential energy function in terms of distance from the origin is given by,
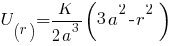 for 0 ≤ r ≤ a
for 0 ≤ r ≤ a
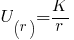 for r ≥ a where K>0 is a positive constant.
for r ≥ a where K>0 is a positive constant.
(a) Derive the force F(r) and determine whether it is repulsive or attractive.
(b) With what velocity should the particle start at r = ∞ to cross over to other side of the origin.
(c) If the velocity of the particle at r = ∞ is 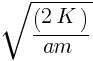 towards the origin describe the motion.
towards the origin describe the motion.
Solution:
(a) F(r) = ? Nature of force whether it is repulsive or attractive =?
Concept: 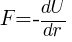
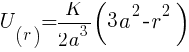
Differentiating above equation wrt dr
For 0 ≤ r ≤ a ![F= - {dU}/{dr} = - {d}/{dr} [{K}/{2a^3}{(3a^2-r^2)}] F= - {dU}/{dr} = - {d}/{dr} [{K}/{2a^3}{(3a^2-r^2)}]](https://mywebpathshala.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_974.5_0331e2de87892e8b5a64e4bb693b54bf.png)
![F = - {d}/{dr} [{K}/{2a^3}{(0 - 2r)}] F = - {d}/{dr} [{K}/{2a^3}{(0 - 2r)}]](https://mywebpathshala.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_974.5_45f6327d443c67ee8093622f1c075955.png)
![F = [{K r}/{a^3}] F = [{K r}/{a^3}]](https://mywebpathshala.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_974.5_754dd9fe7a86ceae84970b71f178f9f8.png) F is positive.
F is positive.
For r ≥ a
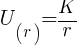
Differentiating above equation wrt dr
![F= - {dU}/{dr} = - {d}/{dr} [{K}/{r}] F= - {dU}/{dr} = - {d}/{dr} [{K}/{r}]](https://mywebpathshala.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_970_6cce83d34d84d72eaaa5f10e738ebee6.png)
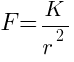 F is positive.
F is positive.
From above it is clear that F is positive in both cases so Force is repulsive in nature.
(b) at r = ∞ v = ? just to cross over to the other side of the origin.
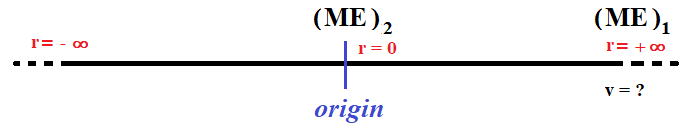
From Law of conservation of energy,
(ME)1 = (ME)2
(ME)1 = KE + PE
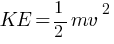
PE =?
For r ≥ a 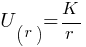
so, at r = ∞ U = 0
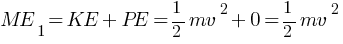
(ME)2 = KE + PE
KE = 0 ( as velocity of particle should be equal to zero, just to pass other side of origin )
At origin PE = ?
For 0 ≤ r ≤ a 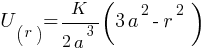
at origin r = 0
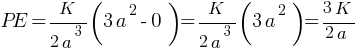
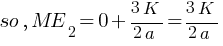
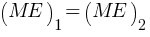
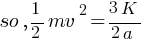
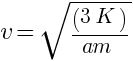

Table of Contents
Question 2: 👇
A single conservative force F(x) acts on a 1.0 kg particle that moves along the x-axis. The potential energy U(x) is given by: U(x)= 20 + (x–2)2 where x is in meters. At x = 5.0 m the particle has a kinetic energy of 20 J.
(i) What is the mechanical energy of the system?
(ii) Make a plot of U(x) as a function of x for –10 m < x < 10 m, and on the same graph draw the line that represents the mechanical energy of the system.
Use part (ii) to determine
(iii) The least value of x.
(iv) The greatest value of x between which the particle can move.
(v) The maximum kinetic energy of the particle.
(vi) The value of x at which it occurs.
(vii) Determine the equation for F (x) as a function of x.
(viii) For what value of x does F(x) = 0 ?
Solution:
(i) at x = 5m KE = 20J Find ME = ?
ME = KE + PE
To find ME, first of all we have to find PE, (U) = ?
U(x) = 20+(x–2)2
at x = 5m U(5) = 20+(5–2)2 = 29J
So, total mechanical energy (ME) = KE + PE = 20 + 29 = 49J
(ii) Plot U(x) as a function of x, for -10m < x < 10m
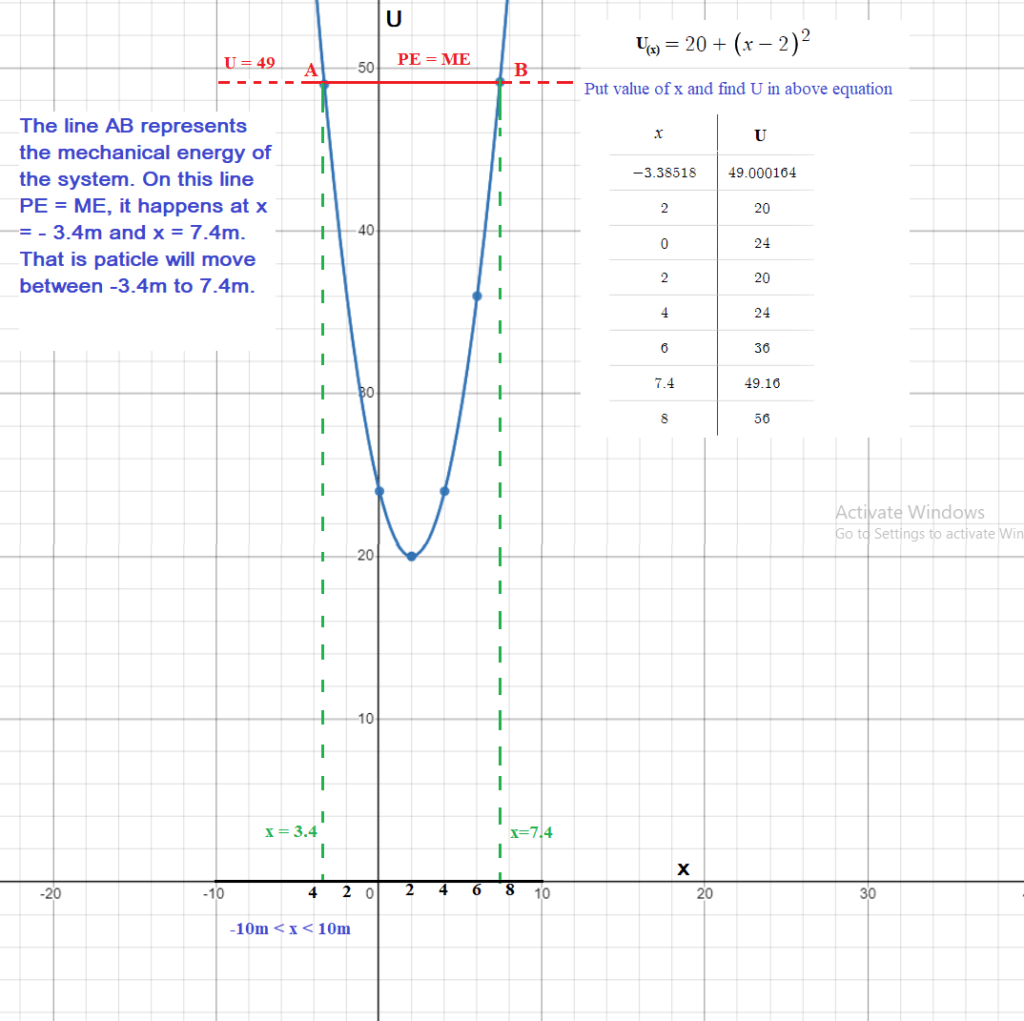
Use part (ii) to solve next part,
(iii) The least value of x = ?
from graph x = -3.4m
(iv) The greatest value of x = ?
from graph x = 7.4m
(iv) Maximum KE = ?
For maximum kinetic energy , potential energy should be minimum (Law of conservation of energy)
from graph minimum value of potential energy = 20J
Total mechanical energy = 49J
So, maximum value of KE = ME – PE = 49J – 20J = 29J
(vi) KE is maximum and potential energy is minimum at x = 2m. { from par (v)}
(vii) F(x) = ? F(x) = – dU/dx
F(x) = (2X – 4) N
(viii) When F(x) = 0 x = ?
F(x) = 2x – 4
0 = 2x – 4
x = 2m
You can see in graph also, slope of U-x graph (dU/dx) is zero at x = 2m
Question 3: 👇
A box having mass 400 kg is to be slowly slide through 10 m on a horizontal state track having friction coefficient 0.2 with the box. (a) Find the work done by the person pulling the box with a rope at an angle θ with the horizontal. (b) Find the work when the person has chosen a value of θ which ensures him the minimum magnitude of the force. (g = 10m/s²)
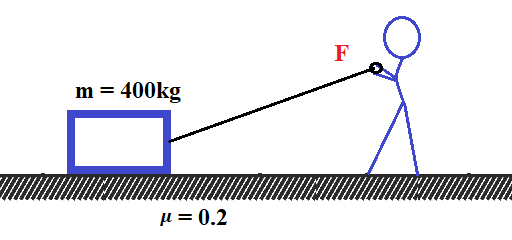
Solution: (a)
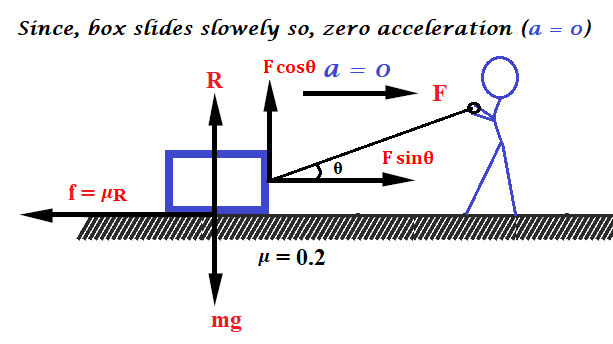
at equilibrium condition,
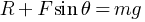
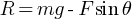 ………………(1)
………………(1)
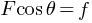 ……………………(2)
……………………(2)
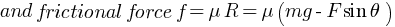
putting value of f in equation (2)
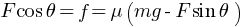
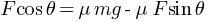
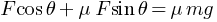
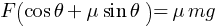
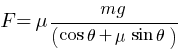
Work done by the person pulling the box with a rope at an angle θ with the horizontal,
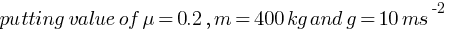
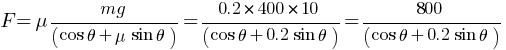
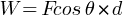
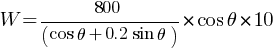
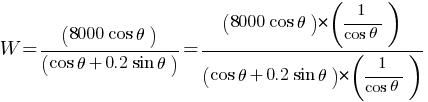
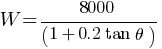
(b) minimum magnitude of the force = ?
Find 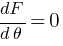
A box having mass 400 kg is to be slowly slide through 10 m on a horizontal state track having friction coefficient 0.2 with the box. Find the work done by the person pulling the box with a rope at an angle θ with the horizontal.
Question 4: 👇
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall. The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one-fourth of the natural length and the block is released. Find its velocity as a function of its distance x from the wall and the maximum velocity of the block. The block is not attached to the spring.
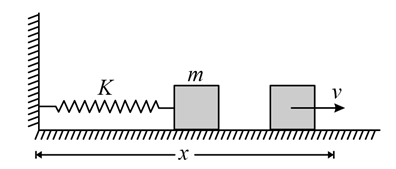
Solution:
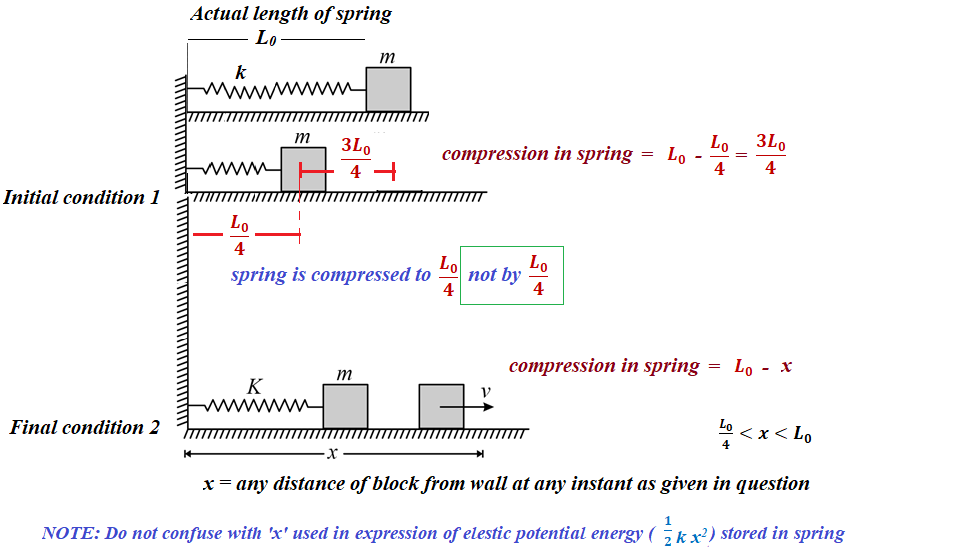
After compression of spring to length 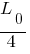 , spring is released, velocity of block will be different when (i) block is in contact with spring
, spring is released, velocity of block will be different when (i) block is in contact with spring 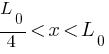 and (ii) contact break
and (ii) contact break 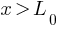 , block will move freely.
, block will move freely.
For 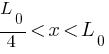
From conservation of energy,
Mechanical energy when spring is compressed = Mechanical energy when spring is released
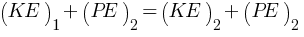
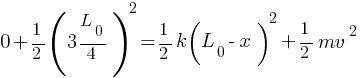
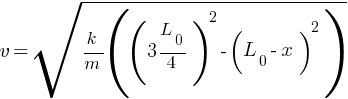
For 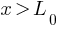
From conservation of energy,
Mechanical energy when spring is compressed = Mechanical energy when spring is released and block move freely = KE of block
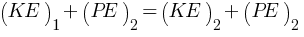
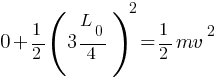
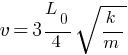
Question 5: 👇
Question 6: 👇
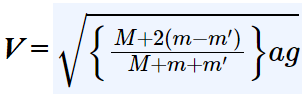
Question 7: 👇
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8
A box having mass 400 kg is to be slowly slide through 10 m on a horizontal state track having friction coefficient 0.2 with the box. Find the work done by the person pulling the box with a rope at an angle θ with the horizontal. A box having mass 400 kg is to be slowly slide through 10 m on a horizontal state track having friction coefficient 0.2 with the box. Find the work done by the person pulling the box with a rope at an angle θ with the horizontal.
Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical, Work Energy and Power Numerical