Spectral Series of Hydrogen Atom
Table of Contents
From Bohr’s Theory energy of an electron in nth orbit is given by,
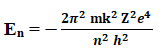
According to Bohr’s postulates (frequency condition) when an electron jump from higher energy level (n2) to lower energy level (n1), energy is released in the form of radiation with frequency ν or wavelength λ,

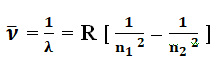
2π2 m k2 Z2e4 / c h3 is called Rydberg constant represented by symbol R and its value is R = 1.0973 × 107 m-1.
Above formula is called Rydberg’s Formula. Rydberg’s Formula is a relationship that explains the spectral series of the hydrogen atom. These spectral series occur due to the transition of electrons from different outer orbits to the inner orbit.
The spectral series of the hydrogen atom describes the distinctive patterns of electromagnetic radiation that hydrogen emits or absorbs as its electrons transit between different energy levels. These spectral series are characterized by distinct wavelengths or frequencies of light, which correspond to different energy differences between the electronic orbits.
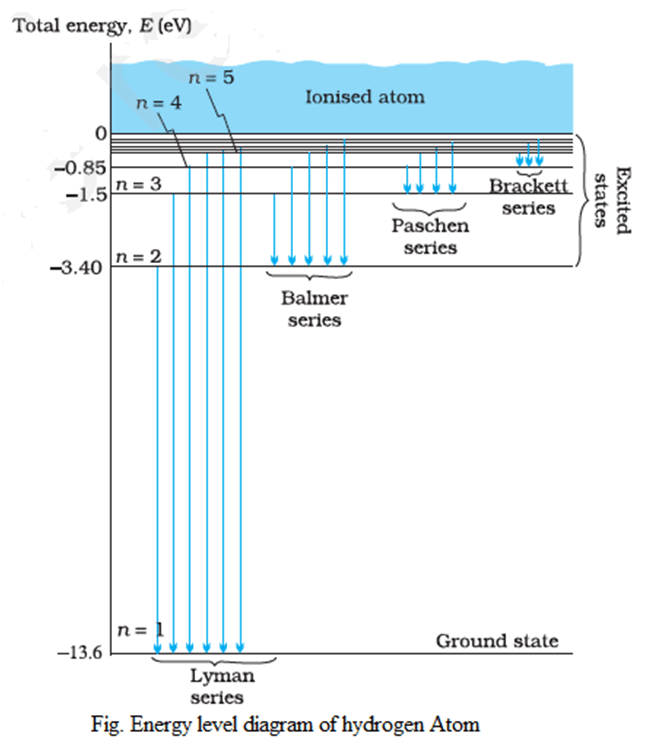
The prominent spectral series of hydrogen include the Lyman series, Balmer series, Paschen series, Brackett series, and Pfund series, each representing transitions to or from the ground state (lowest energy level) and higher energy levels.
Energy Level Diagram for Hydrogen
The Energy Level Diagram for hydrogen is a graphical representation where the energies of the various stationary orbits of an atom are depicted as parallel horizontal lines. These lines are drawn based on a suitable energy scale to illustrate the relative energy levels.
According to Bohr’s theory, the total energy of an electron in nth orbit is given by,
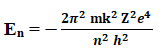
For hydrogen (Z = 1), energy of the electron in the first orbit (n = 1) is given by,
E1 = 2 × (3.14)2 × (9.11 × 10-31 × (9 × 109)2 × (1.6 × 10-19)4/ (6.63 × 10-34)2.12 = – 21.76 × 10-19 J
= – 21.76 × 10-19 / 1.6 × 10-19 eV
E1 = -13.6eV
So, expression for total energy of an electron in nth orbit may be written as,
En = E1/n2 = -13.6/n2 eV
E1 = -13.6/12 = – 13.6 eV
E2 = 13.6/22 = – 3.4 eV
E3 = -13.6/32 = – 1.51 eV
E4 = -13.6/42 = -0.85 eV
E5 = -13.6/52 = -0.54 eV
Thus, When an electron revolves in different orbits, it can possess only specific and distinct values of energy. This phenomenon is referred to as energy quantization, where the energy of the electron is restricted to discrete levels corresponding to the allowed orbits.
Excitation energy:
Excitation energy refers to the energy needed by an electron to transition from the ground state (n1 = 1) to an excited state (n2 = 2, 3, 4, ……………. ).
In the case of hydrogen,
First excitation energy (n1 = 1 n2 = 2) can be calculated by = E2 – E1 = – 3.4 – (-13.6) = 10.2 eV
Second excitation energy (n1 = 1 n2 = 3) of hydrogen = E3 – E1 = -1.51- (-13.6) = 12.09 eV
Excitation potential:
Excitation potential refers to the accelerating potential that provides energy to an electron, enabling it to transition from an inner orbit to an outer orbit.
First excitation potential of hydrogen = – 3.4- (-13.6) = 10.2 V
Second excitation potential of hydrogen = – 1.51- (-13.6) = 12.09 V
Ionization energy:
Ionization energy is the amount of energy needed by an electron to simply exit from its orbit.
Ionization energy of hydrogen = – E1 = 0 – (-13.6) = 13.6 eV
Ionization potential:
The ionization potential refers to the accelerating potential that provides the necessary energy for an electron to completely escape from an atom. It represents the minimum potential difference required to overcome the attractive forces of the nucleus and allow the electron to break free from its bound state within the atom.
First excitation potential of hydrogen = 0 – (-13.6) = 13.6 V
Limitations of Bohr’s Theory
- This theory is only applicable to hydrogen-like atoms with a single electron and is not successful in explaining the behavior of atoms with two or more electrons.
- It does not provide an explanation for the preference of circular orbits over elliptical orbits, despite the possibility of both.
- Bohr’s theory does not provide information about the relative intensities of different spectral lines. It solely predicts the frequencies of these lines.
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ
Spectral Series of Hydrogen Atom, Spectral Series of Hydrogen Atom, Spectral Series of Hydrogen Atom, Spectral Series of Hydrogen Atom, Spectral Series of Hydrogen Atom, Spectral Series of Hydrogen Atom