Hello, readers 😊! Here is important questions from topic displacement current. Show that displacement current is equal to conduction current during the charging of a capacitor.
Show that displacement current is equal to conduction current during the charging of a capacitor.
Answer: Consider a capacitor having capacitance C and plate area A, which is being charged at an instant during the charging of the capacitor. The magnitude of charge on the plates of the capacitor is Q.
The electric field between the plates of a capacitor is given by
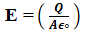
The electric flux passing through the plates of the capacitor is
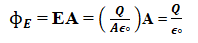
As displacement current is given by,
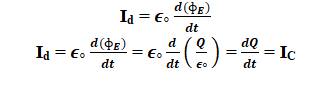
dq/dt is the rate at which charge enters the capacitor’s positive plate via the conducting wire, which is equal to the conduction current.
Table of Contents
Write the properties of Displacement Current.
Ans: Properties of Displacement Current are,
- Displacement current exists when there is a change of electric flux. Unlike conduction current, it does not exist under steady conditions.
- It is not a current. It only adds to current density in Ampere’s Circuital law. As it produces magnetic field, so called current.
Write the difference between Conduction Current and Displacement Current.
Answer: Difference between Conduction Current and Displacement Current,
| Conduction Current | Displacement Current |
|---|---|
| Conduction Current is due to the flow of electrons in a conductor. | Displacement Current is produced due to time-varying electric field. |
| Conduction Current exists even if electrons flow at a uniform rate | Displacement Current does not exist under steady conditions. |
Why does a galvanometer when connected in series with a capacitor show momentary deflection, when it is being charged or discharged? How does this observation lead to modifying the Ampere’s circuital law? Hence write the generalize expression of Ampere’s law.
Answer: When a galvanometer is connected in series with a capacitor, it shows momentary deflection because of the transient current that arises due to the charging or discharging of the capacitor. Initially, when the capacitor starts charging, it acts like a short circuit (low resistance), allowing a large current to flow. As the capacitor tends to fully charge, its voltage increases and the current gradually decreases; the reverse is observed during discharging. When a capacitor becomes fully charged or discharged, the current in the circuit becomes constant or zero, and the galvanometer shows no deflection because the capacitor offers infinite resistance for constant current flow.
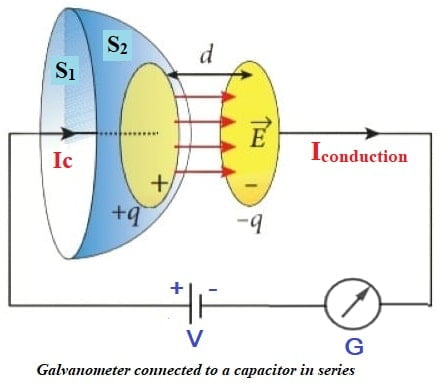
Apply Ampere’s circuital law for the loop at surface S1
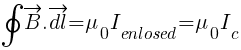…………………. (1)
Now apply Ampere’s circuital law for second face S2 of loop, as no conduction current flow between the plates of capacitor so the line integral of magnetic field at S2 should be equal to zero.
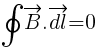…………………. (2)
Since both loop S1 and S2 are very close to each other so equation 1 should be equal to equation 2, but both are not equal so there is a contradiction arises. This contradiction arises by using Ampere’s circuital law, so Ampere’s circuital seems to be inconsistent in this case i.e. this law must be missing something. Maxwell’s find this missing term as displacement current. So modified form of Ampere’s circuital law is,
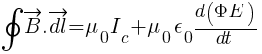…………………. modified form of Ampere’s circuital law
This modified expression of Ampere’s law allows us to consider both conduction currents and displacement currents making it more comprehensive and accurate in describing electromagnetic phenomena involving time-varying electric fields and charging and discharging capacitors.
When an ideal capacitor is charged by a DC battery, no current flows. However, when an AC source is used, the current flows continuously. How does one explain this, based on the concept of displacement current?
Answer: Displacement current establishes continuity of current between the capacitor plates. Displacement current is caused by changes in electric flux between the plates of the capacitor.
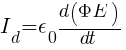
When an ideal capacitor is charged by direct current, there is no change in electric flux, i.e., there is no displacement current. As a result, there is no continuity in the circuit; the capacitor does not conduct direct current.
For an alternating current source, the voltage between the capacitor plates keeps on changing. Due to which, electric flux changes and displacement current arises, which maintains the continuity of the circuit and the capacitor conducts alternate current.
Click here 🖱️ 👉EM Waves MCQs
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ
Show that displacement current is equal to conduction current during the charging of a capacitor. Show that displacement current is equal to conduction current during the charging of a capacitor. Show that displacement current is equal to conduction current during the charging of a capacitor. Show that displacement current is equal to conduction current during the charging of a capacitor.
Show that displacement current is equal to conduction current during the charging of a capacitor. Show that displacement current is equal to conduction current during the charging of a capacitor. Show that displacement current is equal to conduction current during the charging of a capacitor.