Hello, readers😊 ! Here you can learn about system of Units, some Practical Units in Measurement like Light year, Astronomical unit, Parsec, Shake, Lunar month, Solar day, Sedrial day etc. and some practical methods of Measurement of length. significant figures.
System of Units
A system of Units is a complete set of units that is used for measurements of fundamental and derived physical quantities.
A few common systems of units are,
- CGS System: It is also called Gaussian System of units. In this system unit of length is Centimeter, unit of mass is Gram and unit of time is Second.
- FPS System: It is British system of units. In this system unit of length is Foot, unit of mass is Poundand unit of time is Second.
- MKS System: It is French system of units. In this system unit of length is Meter, unit of mass is Kilogramand unit of time is Second.
- SI System: It is similar to French system (MKS) of units abbreviated from French name Le systeme International d Unites. This system is accepted by International Bureau of Weight and Measures in 1971 and in India 1976.
There are 7 fundamental physical quantities in SI units,
| Sr. No. | Physical quantities | Units | Units Symbol |
|---|---|---|---|
| 1 | Length | meter | m |
| 2 | Mass | kilogram | kg |
| 3 | Time | second | s |
| 4 | Current | ampere | A |
| 5 | Temperature | kelvin | K |
| 6 | Amount of substance | mole | mol |
| 7 | Luminous intensity | candela | cd |
Table of Contents
Besides these 7 fundamental quantities there are two other supplementary physical quantities,
| Sr. No. | Physical quantities | Units | Units Symbol |
|---|---|---|---|
| 1 | Plane angle | radian | rad |
| 2 | Solid angle | steradian | st |
Advantage of SI Units:
- It is a coherent system of units: It means all derived unites can be obtained by simple multiplication or division of fundamental units without introducing any numerical factor.
- It is rational system of units: It uses only one unit for a given physical quantity. Eg. Joule is the unit of all type energy.
- It is a metric system: Multiples and sub-multiples of SI units can be expressed as powers of 10.
- It is an absolute system of units: It does not use gravitational unit(g).
- It is internationally accepted system of units.
Practical Units in Measurement
(a) Practical units for small length measurement:
Fermi – used to measure nuclear size. 1fermi = 10-15m
Angstrom – used to measure diameter of atom. 1Angastrom = 10-10m
Micron – used to measure size of microbes. 1micron = 10-6m
(b) Practical units for large distance measurement:
Light Year:
It is the distance traveled by light in one year.
1 light Year = speed of light in vacuum x time = 3 x 108 x 365.25 x 24 x 60 x 60 = 9.467 x 1015m
1ly = 9.467 x 1015m
Astronomical unit:
It is the mean distance from sun to earth.
1AU= 3 x 108 m/s x 500 s = 1.5 x 1011m
1AU = 1.5 x 1011m
Parsec / Parallactic second :
Parallactic second or parsec is the distance at which an arc length of 1 AU subtends an angle of 1” second of arc.
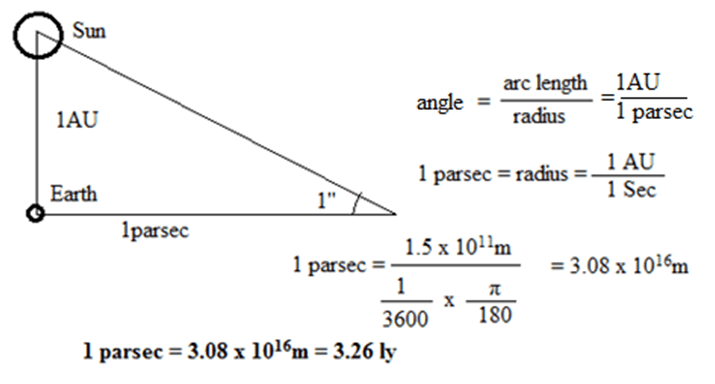
Practical units for measuring time:
Shake – smallest practical unit of time 1shake = 10-8s
Lunar month – It is time taken by moon to complete one revolution around the earth in its orbit.
Solar day: It is the time taken by the earth to complete one rotation about its own axis w.r.t. the sun.
Sedrial day: It is the time taken by the earth to complete one rotation about its own axis w.r.t. a distant star.
Measurement of length:
(a) Direct Method: Length can be measured directly by using meter scale, Vernier Callipers, screw-gauge or Spherometre.
(b) Indirect Method: (i) Measurement of distance of a planet using Kepler’s third law of planetary motion (ii) Reflection or Echo method (iii) Parallax method
(i) Measurement of distance of a planet using Kepler’s third law of planetary motion:
According to this law the square of the time period T of a planet revolving around sun is directly proportional to cube of the semi-major axis R of its orbit.
T2 ∝ R3
By knowing time period of a planet revolving around sun we can find its distance from earth using Kepler’s third law.
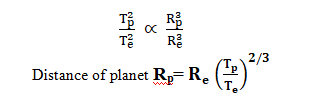
Rp – Semi-major axis of planet Tp – Time period of planet revolving around sun
Re– Semi-major axis of earth Te – Time period of earth revolving around sun
(ii) Reflection or Echo method:
Reflection method is based on echo-ranging and used to measure distance of a hill, depth of a sea and distance of an obstacle. This method is used in SONAR and RADAR. A wave is sent towards an obstacle by transmitter and reflected wave is detected by a receiver, time taken in sending and receiving is measured by a timer circuit. By measuring time and knowing speed of wave in that medium we can measure distance of obstacle.
Distance = v × t / 2 v- Speed of wave in a medium
(iii) Parallax method
Apparent shift in position of an object with respect to another when we see it sidewise (left/right) is called parallax.
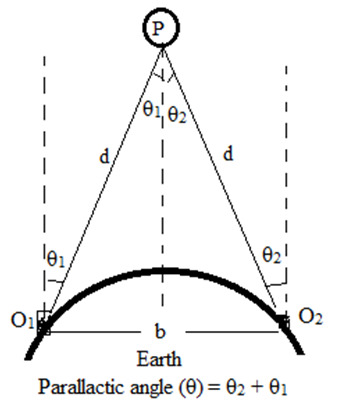
Measurement of distance of moon or any planet:
To measure distance of a planet P which is d distance away from surface of earth, there are two observatories O1 and O2 at separation of b on the surface of earth. Two angle θ1 and θ2 are measured from two observatories using telescope, thus we can measure parallactic angle(θ).
Parallactic angle(θ) = arc length (b) / radius (d)
Distance of planet from surface of earth (d)
d = arc length (b) / Parallactic angle(θ)
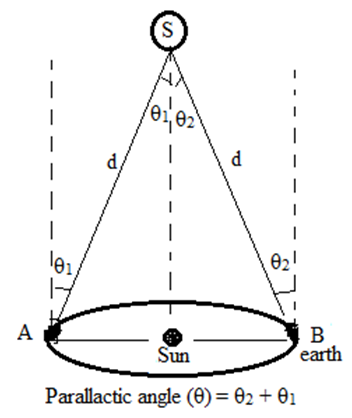
Measurement of distance of a nearby star:
Suppose a nearby star S is at d distance away from earth which position and direction is fixed from earth. When earth is at position A on its elliptical orbit θ1 is measured after six month earth is at diametrically opposite position B, θ2 is measured and hence parallactic angle(θ).
Parallactic angle(θ) = Arc length (AB) / Radius (d)
Distance of star from surface of earth (d)
d = arc length (AB) / Parallactic angle (θ)
Significant Figures
The number of digit in a measurement in which we have confidence in a measurement plus one which is uncertain is called Significant Figures .
OR
All the digits of a measurement that you are sure of (markings on the instrument) plus one estimated digit.
Larger the number of significant figures, greater is the accuracy of the measurement.
Rules for significant digits:
- All Non zero digits are always significant. Example: 5.67 ——————- 3
- All zeros used after the decimal points are significant. Example: 5.60 ———————-3 0.566—————– 3 0.0561 —————- 3
- Zeros between two other significant digits are always significant. Example: 5006 —– 4, 5.006 —– 4
- Zeros used right after the non zero digit are not significant. Example: 56,100 — 3, 56,100 m ——— 5
- Significant figure does not depend on system of units. Example: 56.1cm = 0.561m = 0.000561 Km ——- 3
Rules for calculating with significant figures:
Addition or Subtraction: Round off the answer so that it has the same number of decimal places as the measurement having the fewest/lowest decimal places.
Example: 42.253 mL+125.6 mL + 1.75 mL = 169.603 mL = 169.6mL
Multiplication and Division: Round the answer so that it has the same number of significant digit as the measurement having the fewest/lowest significant digit. Example: 62 cm x 33.03 cm = 2047.86 cm2 = 2.0 x 10 3 cm2
Video Lecture on Practical Units in Measurement
- This video lectures contains following topics:
- System of Units (CGS System, FPS System, MKS System, SI System, Advantage of SI) from starting to 15.07 min
- Practical Units in Measurement (Light year, Astronomical unit, Parsec ) at 15.08 min
- Significant figures at 25.59 min
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ
Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement, Practical Units in Measurement