LCM questions for class 5
Table of Contents
लघुत्तम समापवर्त्य (ल० स०)
दो या दो से अधिक दी हुई संख्याओं के सभी गुणजों में से सबसे छोटे गुणज को उन संख्याओं का लघुत्तम समापवर्त्य (ल० स० ) कहते हैं।
लघुत्तम समापवर्त्य (Lowest Common Multiple) को संक्षेप में ल० स० या LCM लिखते है।
लघुत्तम समापवर्त्य (LCM) दो या दो से अधिक संख्याओं का सबसे छोटा समापवर्तक होता है। LCM की गणना के लिए हम प्रत्येक संख्या के अंतर्गत सभी गुणनों के सबसे छोटे समापवर्तक को निकालकर उनका गुणान करते हैं। यदि दो संख्याओं के बीच LCM निकालने की आवश्यकता हो, तो हम संख्याओं के गुणांक के सबसे छोटे समापवर्तक को निकालकर उनका गुणान करते हैं।
संख्याओं का ल० स० निकालने के लिए हम अभाज्य गुणनखंड विधि का प्रयोग करते हैं।
उदाहरण 1: 12 और 10 का ल० स० ज्ञात कीजिए।
हल: 12 और 10 के अभाज्य गुणनखंड लिखिए,
12 = 2 × 2 × 3
10 = 2 × 5
अब हम देखेंगे कि उपरोक्त दोनों संख्याओं के अभाज्य गुणनखंड में कौन सी संख्या अधिकतम कितनी बार आयी है?
जैसे – अभाज्य गुणनखंड 2 अधिकतम दो बार (12 के गुणनखंड में ) आया है।
अभाज्य गुणनखंड 3 केवल एक बार (12 के गुणनखंड में ) आया है।
अभाज्य गुणनखंड 5 केवल एक बार (10 के गुणनखंड में ) आया है।
दी हुई संख्याओं का ल० स० उन खंडों का गुणनफल है जो उन संख्याओं में अधिकतम बार आते है।
अतः इन संख्याओं का ल० स० = 2 × 2 × 3 × 5 = 60
उदाहरण 2 : 2 और 3 का ल० स० ज्ञात कीजिए।
हल: 2 और 3 का LCM निकालने के लिए, हम प्रत्येक संख्या के अंतर्गत सभी गुणनों के सबसे छोटे समापवर्तक को निकालकर उनका गुणान करते हैं। इसके अनुसार, 2 के अंतर्गत 2, 4, 6, 8, 10, … होते हैं और 3 के अंतर्गत 3, 6, 9, 12, 15, … होते हैं। यहां सबसे छोटा समापवर्तक 6 है। इसलिए, 2 और 3 का LCM 6 होगा। अधिक संख्याओं के लिए भी LCM की गणना इसी तरह से की जाती है।
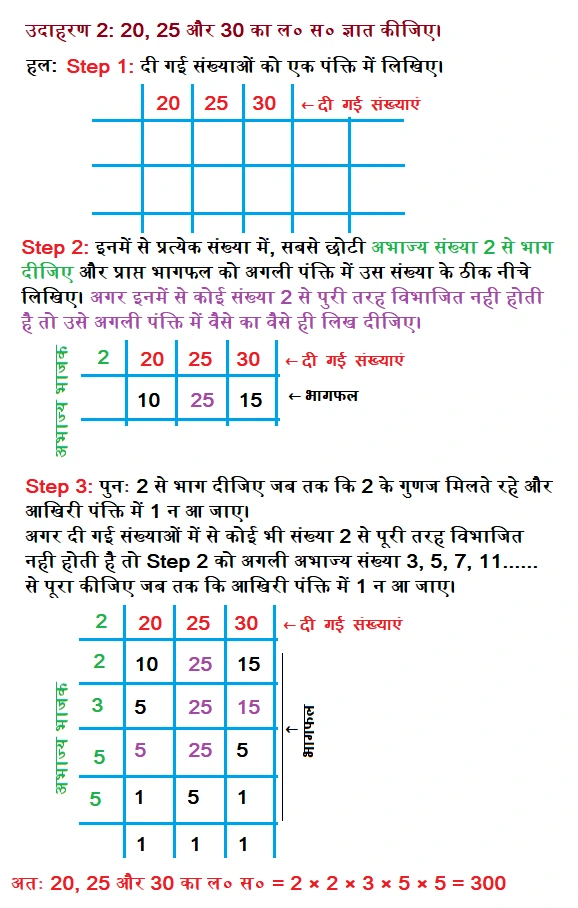
उदाहरण 3 : 20, 25 और 30 का ल० स० ज्ञात कीजिए।
अभ्यास कार्य 1
(1) निम्नलिखित संख्याओं का ल० स० ज्ञात कीजिए।
| (a) 8, 16 | (b) 5, 7 | (c) 18, 27 | (d) 32, 34 |
| (e) 40, 48, 45 | (f) 56, 62, 96 | (g) 144, 132, 120 | (h) 100, 200, 300 |
(2) वह छोटी से छोटी संख्या ज्ञात कीजिए जिसे 12, 16, 24 और 36 से भाग देने पर प्रत्येक दशा में 7 शेष रहता है।
Hint: वह छोटी से छोटी संख्या जो 12, 16, 24 और 36 से पूर्णतया विभाजित हो जाए इन संख्याओं का ल० स० होगी। परंतु उपर्युक्त प्रश्न में हमें ऐसी सबसे छोटी संख्या चाहिए, जिसमें प्रत्येक दशा में 7 शेष रहे अतः वांछित संख्या ल० स० से 7 अधिक होगी।
(3) 6, 8 और 12 से विभाज्य तीन अंकों की सबसे छोटी और सबसे बड़ी संख्या ज्ञात कीजिए।
(4) प्रातः कालीन सैर में, तीन व्यक्ति एक साथ कदम उठाकर चलना प्रारंभ करते हैं। उनके कदमों की लंबाइयाँ क्रमशः 80 सेंटीमीटर, 85 सेंटीमीटर और 90 सेंटीमीटर हैं। इनमें से प्रत्येक न्यूनतम कितनी दूरी चलें कि वह उसे पूरे–पूरे कदमों में तय करें?
Hint: यहाँ प्रत्येक व्यक्ति द्वारा चली गई दूरी को न्यूनतम और समान रहना है अतः वांछित न्यूनतम दूरी उनके कदमों की माप का ल० स० होगा।
लघुत्तम समापवर्त्य (ल० स० ) क्या है?
उत्तर: दो या दो से अधिक दी हुई संख्याओं के सभी गुणजों में से सबसे छोटे गुणज को उन संख्याओं का लघुत्तम समापवर्त्य (ल० स० ) कहते हैं।
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ
LCM questions for class 5, LCM questions for class 5, LCM questions for class 5, LCM questions for class 5