HCF questions for Class 5

महत्तम समापवर्तक (Highest Common Factor)

दो या दो से अधिक संख्याओं का महत्तम समापवर्तक, वह बड़ी से बड़ी संख्या है, जो उन सभी संख्याओं को पूरी तरह विभाजित कर दे।

महत्तम समापवर्तक (Highest Common Factor) को संक्षेप में म० स० प० या HCF लिखते है।

HCF का पूरा नाम “Highest Common Factor” होता है जिसे GCD (Greatest Common Divisor) भी कहा जाता है। यह एक गणितीय अवधारणा है जो दो या अधिक पूर्णांकों के बीच सबसे बड़ी संख्या को ढूंढने के लिए उपयोग किया जाता है, जो कि कोई शेष न छोड़ते हुए उन्हें विभाजित कर सकती है।

संख्याओं का म० स० प० निकालने के लिए हम विभाजन/भाग विधि या अभाज्य गुणनखंड विधि का प्रयोग करते हैं।

महत्तम समापवर्तक क्या है?

उत्तर: दो या दो से अधिक संख्याओं का महत्तम समापवर्तक, वह बड़ी से बड़ी संख्या है, जो उन सभी संख्याओं को पूरी तरह विभाजित कर दे।

दो या अधिक संख्याओं का HCF क्या होता है?

उत्तर: दो या अधिक संख्याओं का HCF वह सबसे बड़ा संख्या होता है जो उन्हें विभाजित कर सकती है और कोई शेष नहीं छोड़ती है।

HCF और LCM के बीच क्या अंतर होता है?

उत्तर: HCF दो या अधिक पूर्णांकों का सबसे बड़ा संख्या होता है जो उन्हें विभाजित कर सकती है और कोई शेष नहीं छोड़ती है, जबकि LCM एक ऐसी सबसे छोटी संख्या होती है जो दो या अधिक पूर्णांकों से बिना शेष छोड़े विभाज्य होती है।

हम दो या अधिक संख्याओं का HCF कैसे ढूंढ सकते हैं?

उत्तर: दो या अधिक संख्याओं का HCF ढूंढने के लकई तरीके हैं, जैसे प्राइम फैक्टराइजेशन, यूक्लिड का एल्गोरिथम, और विभाजन विधि।

प्राइम फैक्टराइजेशन विधि में, हम हर संख्या के प्राइम फैक्टर्स ढूंढते हैं और फिर सामान्य अंशों को ढूंढते हैं।
यूक्लिड का एल्गोरिथम में, हम बड़ी संख्या को छोटी संख्या से बार-बार विभाजित करते हुए जाते हैं जब तक शेष शून्य नहीं होता है। आखिरी न केवल शून्य शेष होता है, उस संख्या को हम HCF मानते हैं।
विभाजन विधि में, हम बड़ी संख्या को छोटी संख्या से विभाजित करते हैं, बचा हुआ शेष लेते हैं, और फिर शेष संख्या को छोटी संख्या से विभाजित करते हैं। इस प्रक्रिया को शून्य शेष मिलने तक दोहराते हुए हम HCF पा सकते हैं।

भाग विधि से म० स० प० ज्ञात करना (Division Method to find HCF)

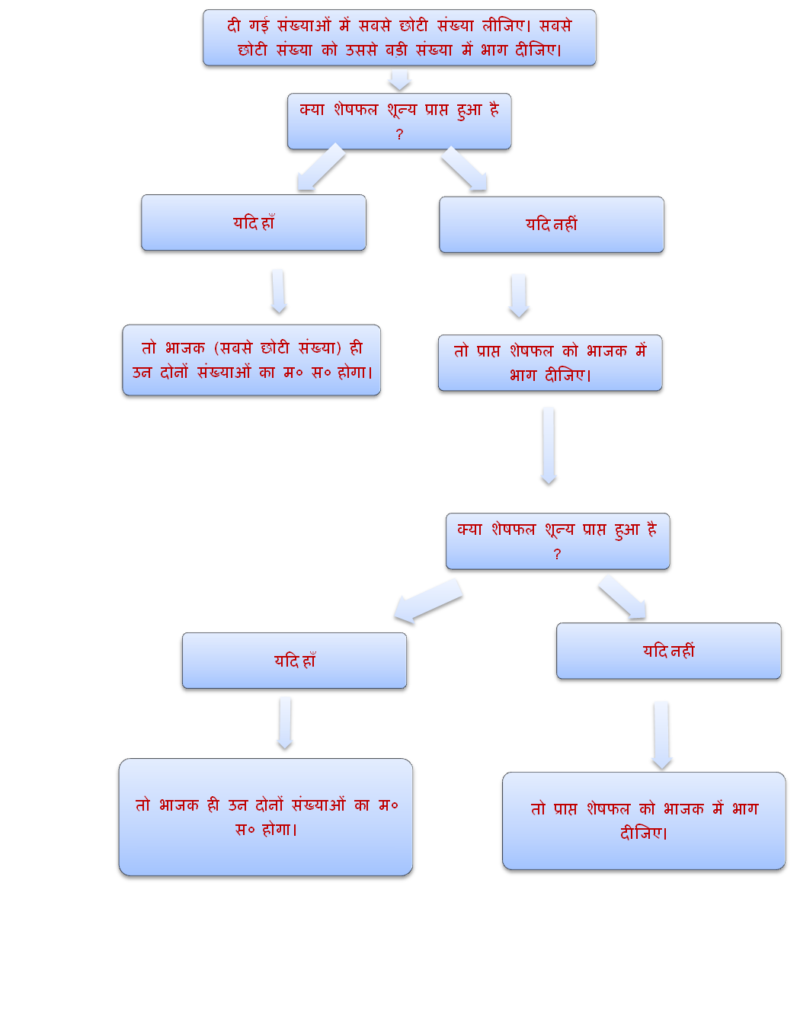
अभ्यास कार्य 1 / Exercise 1

(i) सही(✔️) गलत (❌) का निशान लगाइए।

दो संख्याओं का म० स० प० हमेशा, उन दोनो संख्याओं में से सबसे छोटी संख्या के बराबर या उससे भी छोटा होता है।
दो संख्याओं का म० स० प० हमेशा, उन दोनो संख्याओं में से सबसे बड़ी संख्या के बराबर या उससे भी बड़ा होता है।
दो क्रमागत सम संख्याओं का म० स० प० 1 होगा।
दो क्रमागत विषम संख्याओं का म० स० प० 1 होगा।

(ii) खाली स्थान को भरिए–

यदि दो संख्याओं का म० स० प० 1 है, तो वे संख्याएं ………………. संख्याएँ कहलाती हैं।
दो संख्याओं का म० स० प० उनमें से सबसे छोटी संख्या के बराबर तो हो सकता है लेकिन उससे ………….. नहीं हो सकता।
दो क्रमागत संख्याओं का म० स० प० हमेशा ……….. होता है।

(iii) गुणनखंड विधि का प्रयोग करके निम्नलिखित संख्याओं का महत्तम समापवर्तक (HCF) ज्ञात कीजिए।

(a) 18, 48	(b) 30, 42	(c) 18, 60
(d) 27, 63	(e) 36, 84	(f) 34, 102
(g) 70, 105, 175	(h) 91, 112, 49	(i) 18,54, 81
(j) 12, 45, 75	(k) 120, 240, 360	(l) 360, 420, 480

(iv)भाग विधि का प्रयोग करके निम्नलिखित संख्याओं का महत्तम समापवर्तक (Highest Common Factor) ज्ञात कीजिए।

(a) 24, 36	(b) 15, 25, 30	(c) 8, 12
(d) 12, 16, 28	(e) 9, 12, 15	(f) 4, 8, 20

Answers : Exercise 1

(i) सही(✔️) गलत (❌) का निशान लगाइए।

दो संख्याओं का म० स० प० हमेशा, उन दोनो संख्याओं में से सबसे छोटी संख्या के बराबर या उससे भी छोटा होता है।✔️
दो संख्याओं का म० स० प० हमेशा, उन दोनो संख्याओं में से सबसे बड़ी संख्या के बराबर या उससे भी बड़ा होता है।❌
दो क्रमागत सम संख्याओं का म० स० प० 1 होगा। ❌
दो क्रमागत विषम संख्याओं का म० स० प० 1 होगा। ✔️

(ii) खाली स्थान को भरिए–

यदि दो संख्याओं का म० स० प० 1 है, तो वे संख्याएं ………सह–अभाज्य………. संख्याएँ कहलाती हैं।
दो संख्याओं का म० स० प० उनमें से सबसे छोटी संख्या के बराबर तो हो सकता है लेकिन उससे ……बड़ा…….. नहीं हो सकता।
दो क्रमागत संख्याओं का म० स० प० हमेशा …एक…….. होता है।

अभ्यास कार्य 2 / Exercise 2

2 टैंकरों में क्रमशः 850 लीटर और 680 लीटर मिट्टी का तेल आता है। उस बर्तन की अधिकतम धारिता ज्ञात कीजिए, जो इन दोनों टैंकरों के तेल को पूरा–पूरा माप देगा।
Hint: वांछित बर्तन से दोनों टैंकरों के तेल को पूरा–पूरा मापना है।अतः बर्तन की धारिता दोनों टैंकरों की धारिताओं का पूरा–पूरा विभाजक होना चाहिए। साथ ही दोनों टैंकरों के तेल को कम समय में मापने के लिए बर्तन अधिकतम धारिता का भी होना चाहिए। अतः ऐसे बर्तन की अधिकतम धारिता 850 और 680 का म० स० प० होगा।

MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ

HCF questions for Class 5, HCF questions for Class 5, HCF questions for Class 5, HCF questions for Class 5, HCF questions for Class 5

Share the knowledge spread the love...