Geometry Class 5 रेखागणित
रेखागणित: गणित की वह शाखा, जिसके अंतर्गत हम दो या दो से अधिक रेखा खंडों से बनी आकृतियों का अध्ययन करते हैं उसे ज्यामिति कहते है।
ज्यामिति गणित का एक शाखा है जो बिंदुओं, रेखाओं, कोणों, सतहों और ठोस आकारों की गुणधर्मों, संबंधों और मापों का अध्ययन करती है। ज्यामिति के अध्ययन का इतिहास प्राचीन सभ्यताओं जैसे मिस्री, बाबीलोनी और यूनानियों तक जाता है, जिन्होंने आधुनिक ज्यामिति के आधारभूत सिद्धांतों और थियोरम्स का विकास किया।
ज्यामिति के अध्ययन में सबसे प्रसिद्ध ऐतिहासिक व्यक्तित्वों में यूक्लिड नाम का यूनानी गणितज्ञ शामिल है, जिसे तकनीकी रूप से ज्यामिति के लिए पाठ्यपुस्तक के रूप में उपयोग किया जाता है। यूक्लिड की रचना ने परिभाषाएं, अभिगृहित कथन और तार्किक सिद्धांतों का एक कठोर तंत्र स्थापित किया जो ज्यामिति और अन्य गणित क्षेत्रों में गणितीय तर्क के मानकों को तय करता है।
भारत में, ज्यामिति के अध्ययन का एक लंबा और समृद्ध इतिहास है जो वैदिक काल से शुरू होता है। वास्तुशास्त्र और मन्दिर वास्तुकला जैसी कलाओं में भारतीय ज्यामिति का उपयोग देखा जाता है। भारत में ज्यामिति का अध्ययन समुद्र के किनारों, गुफाओं, महलों और पुरातत्वों में से कई भौगोलिक स्थानों के सूचना संग्रह के लिए उपयोग किया जाता है। आर्यभट्ट, भारतीय गणित के एक प्रसिद्ध वैज्ञानिक थे, जिन्होंने 5वीं शताब्दी में ज्यामिति के लिए सर्वाधिक महत्वपूर्ण ग्रंथ “आर्यभट्टीय” लिखा था। इस ग्रंथ में उन्होंने ज्यामिति के नियमों को विस्तार से वर्णन किया था। भारतीय गणितज्ञ आर्यभट्ट ने भी ज्यामिति के कुछ महत्वपूर्ण सिद्धांतों को प्रस्तुत किया था, जिसमें से समचतुर्भुज और त्रिभुज के क्षेत्रफल के लिए फार्मूले शामिल थे।
आधुनिक समय में, ज्यामिति का अध्ययन और उसका उपयोग विभिन्न क्षेत्रों में होता है, जैसे भूगोल, अंतरिक्ष विज्ञान, इंजीनियरिंग, वास्तुकला और कंप्यूटर ग्राफिक्स।
रेखागणित का परिभाषा क्या है? (What is geometry?)
उत्तर: रेखागणित भौतिक आकृतियों और उनकी गुणधर्मों का अध्ययन है।
ज्यामिति के मूल निर्माण तत्व क्या हैं?
उत्तर: ज्यामिति के मूल निर्माण तत्व बिंदु, रेखा और तल होते हैं।
“ज्यामिति के पिता” किसे कहते हैं? (Who is father of geometry?)
उत्तर: ग्रीक गणितज्ञ यूक्लिड अपनी किताब “Elements” के लिए “ज्यामिति के पिता” कहलाते हैं।
बहुभुज क्या होता है?
उत्तर: बहुभुज एक बंद आकृति होती है, जो सीधी रेखा सेगमेंटों से बनी होती है।
वृत्त और गोला में क्या अंतर है? (What is the difference between circle and sphere?)
उत्तर: वृत्त एक दो-आयामी (2-Dimensional) आकृति होती है जो एक समतल पर बनती है, जबकि गोला एक तीन-आयामी (3-Dimensional) आकृति है जिसमें सभी बिंदु एक केंद्रीय बिंदु से एक समान दूरी पर होते हैं।
Table of Contents
बिंदु (Point):
- किसी कागज़ पर किसी नुकीली पेंसिल की नोक को दबाने से जो चिह्न या निशान (.) प्राप्त होता है, उसे ही बिन्दु कहते है।
- बिंदु की न तो कोई लम्बाई होती है और न ही कोई चौड़ाई होती है।
- बिन्दु का क्षेत्रफल तथा आयतन भी शून्य होता है।

अगर आप कागज़ पर दो बिंदु अंकित करे तो उनमें भेद के लिए उन बिंदुओं को अंग्रेजी या हिंदी वर्णमाला के अक्षरों से निरूपित करने की आवश्यकता होगी।
रेखा (Line):
- एक कागज़ पर किसी नुकीली पेंसिल की सहायता से बहुत सारे बिंदु पास-पास बनाइए। अब इन बिंदुओं को आपस में मिलाते हुए एक पथ खींचिए। इसी ‘पथ’ को रेखा कहते हैं।
- अतः हम कह सकते हैं कि कई सारे बिंदुओं को मिलाने वाले पथ को, रेखा कहते हैं।
- एक रेखा पर अनगिनत बिंदु स्थित होते हैं।
- रेखा अपने दोनों तरफ अंतहीन होती है।
- रेखा की कोई मोटाई नहीं होती (नगण्य) है।

AB एक रेखा हैं जिसकी लंबाई अंतहीन हैं। इस अंतहीन लंबाई को रेखा पर दोनों तरफ तीर (arrow) की मदद से प्रदर्शित करते हैं।
रेखाखंड (Line segment):
रेखा पर स्थित, रेखा का वह भाग जिसका आरंभ और अंत निश्चित होता है उसे रेखाखंड कहते हैं। रेखाखंड की लंबाई निश्चित होती है।

यहाँ CD एक रेखा खंड है।
किरण (Ray):
वह रेखा जिसका आरंभ बिंदु निश्चित हो किंतु अंत, अंतहीन हो उसे किरण कहते हैं।

‘ किरण ‘ AB को हम इस प्रकार प्रदर्शित करते हैं।
किरण को समझने के लिए हम सूर्य की किरणों का सहारा ले रहे हैं। जिस प्रकार सूर्य की किरणें एक निश्चित बिंदु ‘सूर्य’ से प्रारंभ होती हैं और आकाश में अनंत तक फैलती हैं, ठीक उसी प्रकार किरण एक निश्चित बिंदु से प्रारंभ होकर अनंत तक जाती है।
वक्र (curves):
- कागज़ पर पेंसिल की मदद से टेढ़ी-मेढ़ी रेखाएं खींचिए, इस प्रकार प्राप्त आकृति को वक्र कहते हैं।
- आम भाषा में वक्र का अर्थ होता है ‘सीधा नहीं’। गणित में ‘वक्र’ शब्द का प्रयोग ‘सीधी रेखा’ के लिए भी किया जा सकता है।
सरल रेखा (simple line):
पेंसिल द्वारा रूलर की सहायता से खींची गई सीधी रेखा को सरल रेखा कहते हैं।
समांतर रेखाएँ (Parallel lines):
ऐसी सरल रेखाएँ जो एक दूसरे को प्रतिच्छेद नहीं करती या एक दूसरे से अनंत पर भी नहीं मिलती हो समांतर रेखाएं कहलाती हैं।
आप अपने आसपास ऐसे समांतर रेखाएँ आसानी से देख सकते हो जैसे रेल की दोनों पटरियां, जिनके बीच की दूरी हमेशा समान होती हैं तथा एक दूसरे से कही भी नहीं मिलती।

रूलर स्केल के दोनों सम्मुख किनारे जो एक दूसरे से नहीं मिलते तथा इनके बीच की दूरी भी हमेशा समान होती है।
प्रतिच्छेदी रेखाएँ (Intersecting lines):
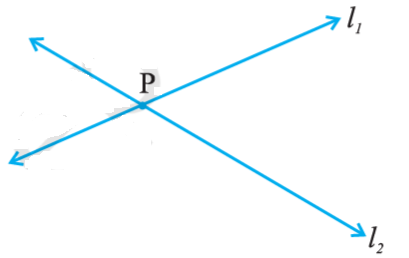
यदि दो रेखाओं में एक उभयनिष्ठ बिंदु (Common point) हो तो वह प्रतिच्छेदी रेखाएँ कहलाती हैं। यहाँ l1 और l2 प्रतिच्छेदी रेखाएँ हैं जहाँ P उभयनिष्ठ बिंदु है।
geometry / rekha ganit
कोण (Angle) के विषय में जानकारी प्राप्त करने के लिए नीचे दिए गए लिंक पर 👇🖱️ क्लिक कीजिए।
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ
Geometry Class 5 रेखागणित, Geometry Class 5 रेखागणित, Geometry Class 5 रेखागणित, Geometry Class 5 रेखागणित, Geometry Class 5 रेखागणित, Geometry Class 5 रेखागणित, Geometry Class 5 रेखागणित
I appreciated your work and the way you presented it here. The design is elegant and the topic is handled with style, but there is a certain harshness that you should address. If you do, I have no doubt that the same issues will continue to arise frequently unless you address this challenge.