Figure 8.6 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm….
Figure 8.6 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A.
(a) Calculate the capacitance and the rate of change of potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor? Explain.
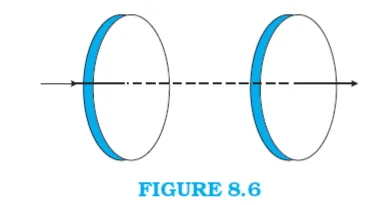
Sol: Given: Radius of capacitor plate R = 12 cm = 12 × 10-2 m
Separation between plates d = 5.00 mm = 5 × 10-3 m
⇒ Area of capacitor plate = πR2 = 3.14 × (12 × 10-2 m) 2 = 4.53 × 10-2 m 2
(a) Capacitance C = ?
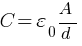
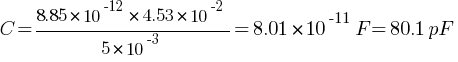
The rate of change of potential difference between the plates (dV/dt) = ?
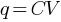
Differentiating this equation with respect to time,
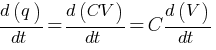
Where, C = Capacitance (constant) 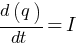
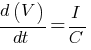
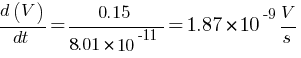
(b) Displacement Current = ?
Conduction Current = charging current = 0.15A
Displacement Current = Conduction Current
Displacement Current = 0.15A
(c) Is Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor?
Yes, Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor as Kirchhoff’s junction rule is based on law of conservation of charge and it is fundamental law of nature.