Equations of motion class 9
Hello, readers ! Here, Equations of motion are given which helps us in analyzing various parameters of motion. Equations of motion class 9.
To describe the motion of an object, we use physical quantities like displacement, velocity, and acceleration. In the case of constant acceleration, the velocity acquired and the displacement travelled in a given time can be calculated by using one or more of three equations. These equations are generally known as equations of motion.
Limitations of Equations of motion :
Limitations of Equations of motion, Equations of motion can be applied only when acceleration is constant during motion.
Table of Contents
Equations of motion 1st:
Consider a body is moving with initial velocity ‘u’, under influence of a force body accelerated with acceleration ‘a’ and its velocity increases to ‘v’ in time ‘t’.
Acceleration body is given by, Acceleration (a) = Change in velocity / Time taken
Acceleration (a) = [Final velocity (v) – Initial velocity (u)] / Time taken for change in velocity (t)
a = (v – u) / t
a t = (v – u)
a t + u = v
v = u + at ………….. (1)
Click here 🖱️👉 Motion NCERT in-text Questions Solution
Equations of motion 2nd:
Consider a body is moving with initial velocity ‘u’, under influence of a force body accelerated with acceleration ‘a’ and its velocity increases to ‘v’ in time ‘t’. Displacement travelled by body is ‘x’.
Displacement travelled by body (x) = Average velocity × time taken
x = ½ (u + v) × t
From equation of motion (1), v = u + at. putting value of ‘v’ in above formula.
x = ½ [u + v] × t = ½ [u + (u + at)] × t
x = ½ [u + u + at] × t = ½ [2u + at)] × t = ½ [2ut + at2]
x = ½ × 2ut + ½ × at2 = ut + ½ at2
x = ut + ½ at2 ………….. (2)
Click here 🖱️👉 Motion NCERT Questions Solution
Equations of motion 3rd:
Consider a body is moving with initial velocity ‘u’, under influence of a force body accelerated with acceleration ‘a’ and its velocity increases to ‘v’ in time ‘t’. Displacement travelled by body is ‘x’.
Displacement travelled by body (x) = Average velocity (vav) × time taken (t) ∵ vav = (u+v)/2
(x) = (vav) × (t) = ½ (u+v) × (t)
Putting value of t, from equation (1) v = u + at ⇒ t = (v – u)/a
x = ½ (u+v) × (t) = ½ (u+v) × (v – u)/a
x = ½ (v2 – u2) / a
2ax = (v2 – u2)
(v2 – u2) = 2ax ……….(3)

Question 1: A car starts from rest and moves along the x-axis with the constant acceleration 5m/s2 for 8s. if it then continue with constant velocity, what will distance the car cover in 12s since it started from rest.
Answer: CONCEPT ☞ In above question speed of car changes (from rest to motion) for 8s, so accelerated motion and then after up to 12s (4s after 8s) velocity is constant so uniform motion.
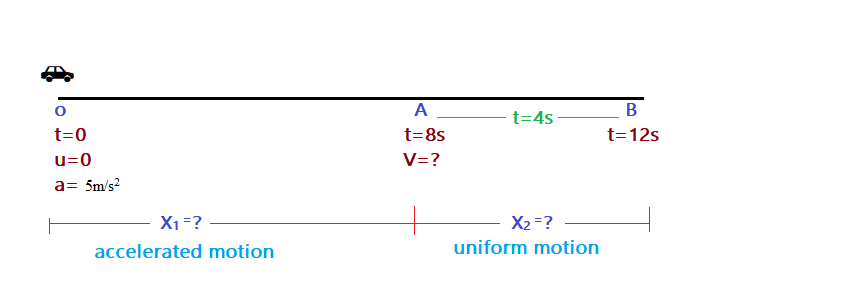
Given: Accelerated motion (O to A)
Initial speed u = 0 (starting from rest)
Time taken t = 8 s
Acceleration (retardation) = 5 m s–2
Final speed v = ?
From equation of motion 1st v = u + at
v = 0 + 5 × 8 = 40 m s–1
Now this speed will be constant for next 4s and motion is uniform motion (A to B)
From equation of motion 2nd x = u t +1/2 at2
X1 = 0 × 10 +1/2 5× (8)2 = 160 m
Uniform motion (A to B)
Displacement = velocity × time taken
X2 = 40 × 4 = 160 m
Total distance travelled in 12 s is X = X1 + X2 = 160m + 160m = 320 m
Question 2: How will the equations of motion for an object moving with uniform velocity change?
Answer: If object is in uniform motion then final velocity (v) = initial velocity (u) and also acceleration (a) = 0. So applying equations of motion, we get
x = u t +1/2 at2 = u t +1/2 (0)t2 = u t +0 = u t
Displacement (x) = velocity (u) × time (t)
We use only this formula to analyze uniform motion while in non-uniform motion we use 3 equations of motion.
Question 3: An electron moving with a velocity of 5 ×104 m/s enters in to an uniform electric field and acquires a uniform acceleration of 104 m/s2 in the direction of its initial motion.
(i)Calculate the time in which electron would acquire a velocity double of initial velocity.
(ii) How much distance the electron would cover in this time?
Ans: Given: Initial velocity u = 5 ×104 m/s
Acceleration a = 104 m/s2
(i) Time =? When, final velocity (v) = initial velocity (u) × 2 = 5 ×104 × 2 = 10×104 m/s
From equation of motion 1st v = u + at
10×104 = 5×104+ 104 t
t = 5 ×104/ 104 = 5s
(ii) Distance covered by electron in 5s X= ?
From equation of motion 2nd x = u t +1/2 at2
X = 5 ×104 × 5 + ½ 104 (5)2 = 37.5 × 104m
Question 4: An object starting from the rest travels 20m in first 2s 160m in next 4s. What would be the velocity after 7s from start?
Answer:
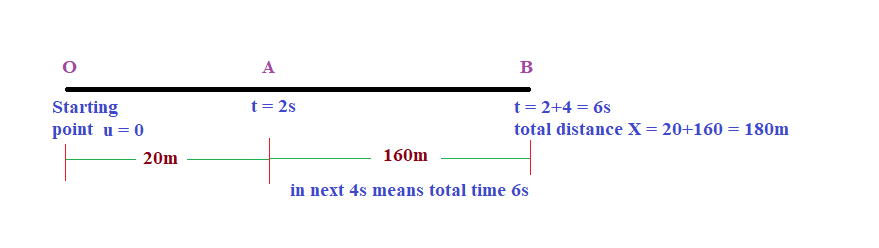
From equation of motion 2nd x = u t +1/2 at2
Distance travelled by object in first 2 second, X1 = 20m u = 0 (starting from the rest)
X1 = u t +1/2 at2 = 0 × 2 + ½ a (2)2 = 2a = 20
a = 10 m/s2
Distance travelled by object in next 4s means total 6 second, X2 = 20 +160= 180m u = 0 (starting from the rest)
X2 = u t +1/2 at2 = 0 × 6 + ½ a (6)2 = 18a = 180
a = 10 m/s2
Velocity after 7s from start,
From equation of motion 1st v = u + at = 0 + 10 × 7= 70m/s
Click here 🖱️👉 Motion Graphs Class 9 Quiz-2
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ