Dual Nature NCERT Solution
Dual Nature NCERT Solution
Find the (a) maximum frequency, and (b) minimum wavelength of X-rays produced by 30 kV electrons.
Answer: (a) maximum frequency = ?
Given 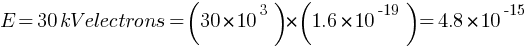 J
J
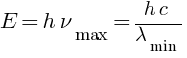
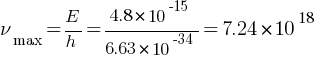 Hz
Hz
(b) minimum wavelength of X-rays = ?
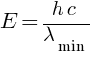
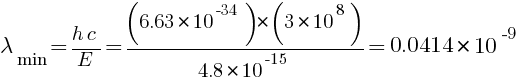 m
m
Table of Contents
The work function of caesium metal is 2.14 eV. When light of frequency 6 ×1014Hz is incident on the metal surface, photoemission of electrons occurs. What is the
(a) maximum kinetic energy of the emitted electrons,
(b) Stopping potential, and
(c) maximum speed of the emitted photoelectrons?
Answer: Given: work function of caesium metal = 2.14 eV , light frequency = 6 ×1014Hz
(a) maximum kinetic energy of the emitted electrons Kmax = ?
Einstein’s photoelectric equation, 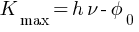
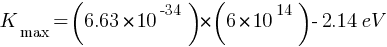
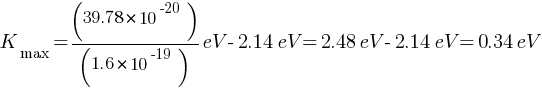
(b) Stopping potential =?
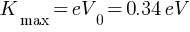
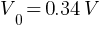
(c) maximum speed of the emitted photoelectrons = ?
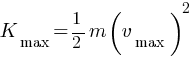
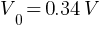
The photoelectric cut-off voltage in a certain experiment is 1.5 V. What is the maximum kinetic energy of photoelectrons emitted?
Answer: Given: V0 = 1.5V
Kmax = ?
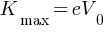
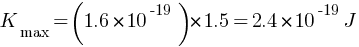
Monochromatic light of wavelength 632.8 nm is produced by a helium-neon laser. The power emitted is 9.42 mW.
(a) Find the energy and momentum of each photon in the light beam,
(b) How many photons per second, on the average, arrive at a target irradiated by this beam? (Assume the beam to have uniform cross-section which is less than the target area), and
(c) How fast does a hydrogen atom have to travel in order to have the same momentum as that of the photon.
Ans: Monochromatic light wavelength = 632.8 nm = 632.8 × 10-3 m, P = 9.42 mW = 9.42 × 10-3 W
(a) energy K = ?, momentum p = ?
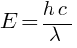
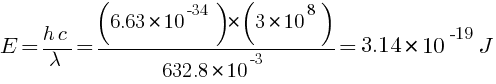
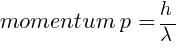
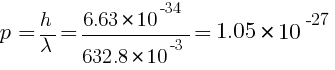 kg m/s
kg m/s
(b) How many photons per second, on the average, arrive at a target irradiated by this beam?
Number of photons per second, on the average, arrive at a target 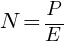
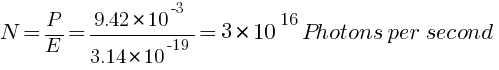
(c) v = ?
momentum of photon = momentum of hydrogen atom
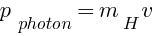
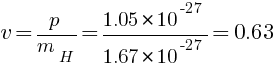 m/s
m/s
The energy flux of sunlight reaching the surface of the earth is 1.388 × 103 W/m2. How many photons (nearly) per square metre are incident on the Earth per second? Assume that the photons in the sunlight have an average wavelength of 550 nm.
Answer: Given: Energy flux of sunlight reaching the surface of the earth (Energy of sun per squire meter per second) = 1.388 × 103 W/m2 {(j / s) / m2}, Wavelength = 550 nm = 550 × 10–9 m
Number of photons per square metre incident on the Earth per second = ?
Energy of each photon 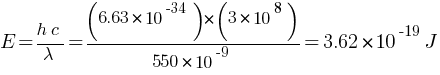

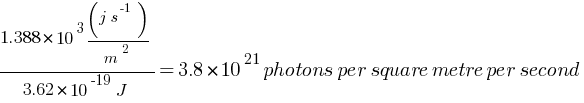
In an experiment on photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be 4.12 × 10–15 V s. Calculate the value of Planck’s constant.
A 100W sodium lamp radiates energy uniformly in all directions. The lamp is located at the centre of a large sphere that absorbs all the sodium light which is incident on it. The wavelength of the sodium light is 589 nm. (a) What is the energy per photon associated with the sodium light? (b) At what rate are the photons delivered to the sphere?
The threshold frequency for a certain metal is 3.3 × 1014 Hz. If light of frequency 8.2 × 1014 Hz is incident on the metal, predict the cutoff voltage for the photoelectric emission.
The work function for a certain metal is 4.2 eV. Will this metal give photoelectric emission for incident radiation of wavelength 330 nm?
Light of frequency 7.21 × 1014 Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 × 105 m/s are ejected from the surface. What is the threshold frequency for photoemission of electrons?
Light of wavelength 488 nm is produced by an argon laser which is used in the photoelectric effect. When light from this spectral line is incident on the emitter, the stopping (cut-off) potential of photoelectrons is 0.38 V. Find the work function of the material
from which the emitter is made.
Calculate the
(a) momentum, and
(b) de Broglie wavelength of the electrons accelerated through a potential difference of 56 V.
What is the
(a) momentum,
(b) speed, and
(c) de Broglie wavelength of an electron with kinetic energy of 120 eV.
The wavelength of light from the spectral emission line of sodium is 589 nm. Find the kinetic energy at which
(a) an electron, and
(b) a neutron, would have the same de Broglie wavelength.
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ
Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution, Dual Nature NCERT Solution