Distance and Displacement
Distance:
- Distance is the total path length traveled by an object during its motion.
- It is a scalar quantity, which means it has only magnitude and not the direction.
- Distance is always positive and is usually measured in units such as meters (m), kilometers (km), or miles (mi).
- To calculate the distance covered, one simply adds up the individual lengths of all the different segments of the path.
- For Example: Think of an automobile driving from point A to point B, then on to point C. The sum of lengths AB and BC would represent the distance covered. The distance stays the same no matter the path followed as long as the endpoints don’t change.
Displacement:
- Displacement is the change in position of an object from its initial point to its final point.
- It is a vector quantity as has both magnitude and direction.
- Displacement can be represented graphically by an arrow, where the length of the arrow corresponds to the magnitude of the displacement, and the direction of the arrow indicates the direction of motion.
- To calculate displacement, one needs to consider the shortest straight-line path between the initial and final positions.
- Depending on the direction of the motion relative to the beginning position, displacement might be positive, negative, or zero.
- For Example: if the car travels from point A to point B and then returns back to point A, the displacement would be zero. This is because the car’s final position is the same as its initial position, even though it covered a certain distance during the journey.
Table of Contents
Difference between Distance and Displacement:

Understanding concept of distance and displacement:
Let’s understand distance and displacement with the help of a simple example. Suppose you are sitting in a square-shaped room (ABCD), with each side length of 10 m. You start moving from the initial point A and go to points B, C, and D further step by step.
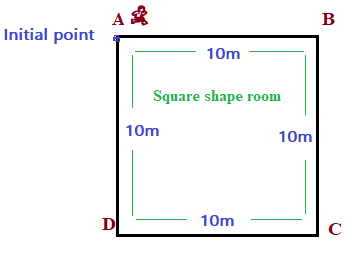
- (i) In first step, you move from corner/point A to B –
- Distance travelled by you will be equal to 10m, as distance is the path length.
- Displacement is also equal to 10m.
Distance = Displacement = 10m
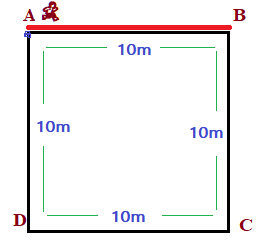
- (ii) In second step, you move from point A to C via B ( A → B → C )
- Distance = 10m + 10m = 20m
- Displacement = 10√2 m
- Using Pythagoras theorem, (AC)2 = (AB)2 + (BC)2
- Displacement = Straight line distance between initial position and final position = (AC) = √ [(AB)2 + (BC)2] = √ [(10)2 + (10)2] = 10√2 m
Distance > Displacement
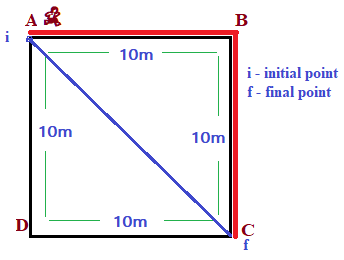
- (iii) In third step, you move from point A to D ( A → B → C → D)
- Distance = 10m + 10m + 10m = 30m
- Displacement = Straight line distance between initial position and final position = AD = 10m
Distance > Displacement
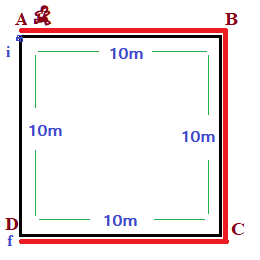
- (iv) In fourth step, you move from point A to A (A → B → C → D→ A)
- Distance = 10m + 10m + 10m + 10m = 40m
- Displacement = Change in position of a body = There is no change in position of body = zero displacement.
- Displacement = 0
Question: The displacement of a moving object in a given interval of time is zero. Would the distance travelled by the object also be zero? Justify your answer.
Ans: If displacement of a moving object in a given interval of time is zero then distance travelled by the object may or may not be zero.
(i) Displacement = 0, distance = 0 ☞ no motion/static condition
(ii) Displacement = 0, distance ≠ 0 ☞ (a) object is in circular motion (b) moving object returns to its initial state/origin after travelling.
Click here 🖱️👉 Motion NCERT Questions Solution
Some important short answer type questions:
Under what conditions distance and displacement of a moving object have the same magnitude?
Answer: The magnitude of distance and displacement of a moving object are same when the object moves along the straight line.
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ