Dimensional Analysis and its Applications

• Home
• Physics
• Physical world and measurement
• Dimensional Analysis

Dimensional Analysis and its Applications

Hello, readers😊! Here we will learn about Dimensional Analysis, how to write dimensional formula, applications of dimensional analysis and Principle of Homogeneity. Methods of dimension analysis was introduced by French Mathematician Joseph Fourier.

Dimensions: The dimensions of a physical quantity are the powers to which the fundamental quantities must be raised to represent the given physical quantity. Example: Density = [M L^-3]

Dimensions of density are 1 in mass, -3 in length and 0 in time.  

Dimensional Formula: The expression which show that which of the fundamental quantities and with what powers enter in to the derived unit of physical quantity is known as dimensional formula of that physical quantity. Dimensional formula of force is [M LT^-2]

Dimensional equation: The equation obtained by equating the symbols of a physical quantity with its dimensional formula is called dimensional equation. Example: F = [MLT^-2], F-force

Dimensional formula of 7 fundamental physical quantities:

There are 7 fundamental physical quantities for which we can write Dimensional formula,

Sr. No.	Physical Quantities	Dimensional formula
1	Mass	[M]
2	Length	[L]
3	Time	[T]
4	Temperature	[K] or [θ]
5	Electric current	[A]  or [I]
6	Luminous intensity	[Cd]
7	Amount of substance	[Mol]

Applications of Dimensional Analysis:

1. To check the correctness of given physics formula.
2. To derive the relationship between various physical quantities.  
3. Conservation of one system of units in to other.

Principle of Homogeneity:

According to this principle if a physics formula is dimensionally correct it must have same dimension on both side (left hand side and right hand side) of that equation.

From the Principle of Homogeneity, it is clear that a physics formula or equation will be dimensionally correct if it has the same dimension on both sides, left-hand side and right-hand side of that equation. For example: distance (s) = velocity (v) × time (t). Here the dimension formula of distance (LHS) is [L] and the dimension formula of velocity (v) × time (t) is also [L], so this physics formula is dimensionally correct.

In other words, a physics formula will be dimensionally correct if two physical quantities which are added or subtracted must have the same dimension, but for multiplication or division, it is not necessary. Let’s understand this with the help of the above example: Distance (s) = velocity (v) × time (t). We can write this formula as, distance (s) -velocity (v) × time (t) = 0. Here, the dimension formula of distance is [L] and the dimension formula of (v × t) is also [L]. Both terms, which are substracted to each other, have the same dimension. So this formula is dimensionally correct.

Note: Logarithmic function (log, ln), trigonometric function (like sin, cos), exponential function (e^x), numerical value (1, 2, 3….) and some constant(π, e) are dimension less.

Physical quantities which are unitless are always dimensionless but physical quantities which are dimensionless may have unit. eg. Plane angle, solid angle.

(1) To check the correctness of given physics formula:

Numerical 1: Check the dimensional correctness of given physics equation s = ut + ½ at². Where, ‘s’ is the displacement, ‘u’ is the initial velocity, ‘a’ is the acceleration and ‘t’ is the time.

Solution:     s = ut + ½ at²

From above, L.H.S = s

and               R.H.S = ut + 1/2at²

The dimensional formula for the L.H.S can be written as, s = [L¹M⁰T⁰] or [L¹] or [ L]  ( since dimensions of M and T are zero in dimension formula of ‘s’)

The dimensional formula for the R.H.S is,  ut + ½ at² = [ L¹T^-1] [ T¹] + [ L¹T^-2] [T¹]² = [ L¹ T⁰] or [ L]

( 👆 do not write 1/2 in dimensional equation because numeric are dimension less)

Comparing dimensional Formula of [ L.H.S] and [ R.H.S], both are equal so, the given equation is dimensionally correct ( By the principle of homogeneity).

(2) To derive the relationship between various physical quantities:

A planet moves around the sun in nearly circular orbit. Its period of revolution T depends on, Radius r of orbit, mass M of sun and gravitational constant G. Show dimensionally that T² ∝ r³.

Solution:

Time period of revolution (T) depends on Radius of orbit (r), mass of sun (M) and gravitational constant (G)

T ∝ r, M, G

As we don’t know about the powers of r, M, and G, we consider their powers a, b, and c, respectively.

T ∝ r^a M^b G^c

removing proportionality (∝) symbol and writing above in the form of equation

T = k r^a M^b G^c …………………………… (1)

Where, k is dimensionless proportionality constant

Dimension formula of Time period T = [T]

Dimension Formula of r = [L]

Dimension Formula of M = [M]

Dimension formula of G = [M^-1 L³ T^-2]

Writing dimension formula in equation (1), k = 1 since dimensionless

[T] = [L]^a [M]^b [M^-1 L³ T^-2]^c

[M⁰ L⁰ T¹] = [L^a M^b M^-c L^3c T^-2c ] = [M^b-c L^a+3c T^-2c ]

Comparing powers of M, L and T from both side,

b – c = 0, a + 3c = 0, -2c = 1

-2c = 1 ⇒ c = -1/2

b – c = 0 ⇒ b = c = -1/2

a + 3c = 0 ⇒ a = – 3c = – 3 × (-1/2) = 3/2 , a = 3/2

putting value of a, b and c in equation (1)

T = k r^a M^b G^c = k r^3/2 M^-1/2 G^-1/2

Squaring both side,

T² = k r³ M^-1 G^-1

From it is clear that T² ∝ r³

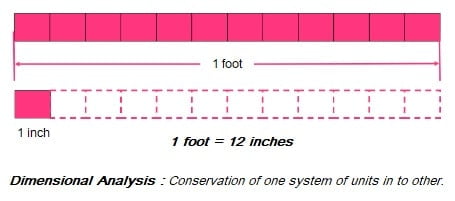
(3) Conservation of one system of units in to other:

Important questions from the Topic

What are the limitations of dimensional analysis?

Answer: Limitations of dimensional analysis are,

1. If a physics formula is dimensional correct it is not necessary that it is experimentally correct also.
2. If a physics formula consist sum or difference of two or more physical quantity we cannot derive it dimensionally. (like v = u+ at )
3. If a physics formula depends on three physical quantities, out of which two have same dimensions, the formula cannot be derived by methods of dimensions.
4. It cannot be applied to derive the relation between various physical quantities if a physical quantity is dependent on more than 3 physical quantities in mechanics.
5. On the basis of dimensional formula only we cannot identify a physical quantity exactly because there are some different physical quantities which have same dimension. eg. Work, energy and torque.   
6. It does not give any information about dimensionless constant.
7. We cannot derive physics formula consisting logarithmic, trigonometric or exponential function by method of dimension.

Check the dimensional correctness of given physics equation W = 1/2 mv² – mgh. Where, ‘W’ is the work done, ‘m’ is the mass, ‘g’ is acceleration due to gravity, ‘v’ is velocity and ‘h’ is height.

To check the above equation as dimensionally correct, we first write dimensions of all the physical quantities mentioned in the equation.

W = Work done = Force × Displacement = [MLT^-2] × [L] = [ML²T^-2]

1/2 mv² = Kinetic Energy = [M] × [L²T^-2] = [ML²T^-2]

mgh = Potential Energy = [M] × [LT^-2] × [L] = [ML²T^-2]

Since all the dimensions on left and right sides are equal it is a dimensionally correct equation.

MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ

Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications,

Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications, Dimensional Analysis and its Applications