A uniform string of mass M and length 2a is placed symmetrically over a smooth and small pulley and has particles of masses m and m' attached to its ends; show that when the string runs off the peg its velocity is ... best

👉 Question 1:

A uniform string of mass M and length 2a is placed symmetrically over a smooth and small pulley and has particles of masses m and m’ attached to its ends; show that when the string runs off the peg its velocity is

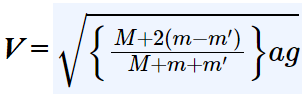
Assume that m> m’.

Solution:

A uniform string of mass M and length 2a, is placed symmetrically over a smooth and small pulley and has particles of masses m and m' attached to its ends; show that when the string runs off the peg its velocity is

👉 Question 2:

Particle 1 experiences a perfectly elastic collision with a stationary particle 2. Determine their mass ratio, if (a) after a head-on collision the particles fly apart in the opposite directions with equal velocities, (b) the particles fly apart symmetrically relative to the initial motion direction of particle 1 with the angle of divergence θ = 60°.

Solution:

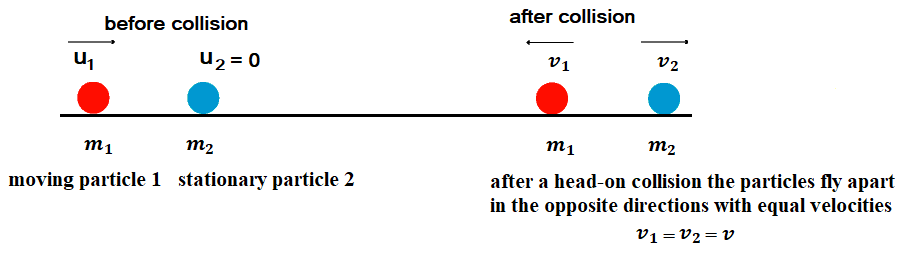
Particle 1 experiences a perfectly elastic collision with a stationary particle 2. Determine their mass ratio, if after a head-on collision the particles fly apart in the opposite directions with equal velocities.

Since, collision is perfect elastic collision so Momentum as well as KE will be conserved,

From momentum conservation,

m₁u₁ + m₂ u₂ = m₁v₁ + m₂ v₂ (initial momentum = final momentum)

since u₂ = 0 and v₁ = – v₂ (after collision both particles move in opposite direction, momentum is a vector quantity so negative sign included here for opposite direction of velocity)

m₁u₁ + m₂ × 0 = m₁v₁ + m₂ (- v₁) = (m₁ + m₂) v₁

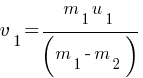$v_1 = {m_1u_1} / (m_1 - m_2)$ ……………….(1)

From KE conservation,

1/2 m_1 (u_1)^2 + 1/2 m_2 (u_2)^2 = 1/2 m_1 (v_1)^2 + 1/2 m_2 (v_2)^2

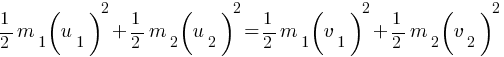
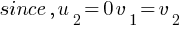since, u_2 = 0 v_1 = v_2 (KE is scalar quantity so negative sign of velocity is not included)

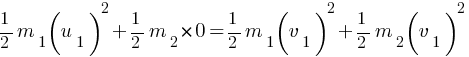
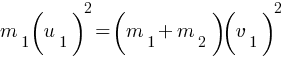1/2 m_1 (u_1)^2 + 1/2 m_2 *0 = 1/2 m_1 (v_1)^2 + 1/2 m_2 (v_1)^2

m_1 (u_1)^2 = (m_1 + m_2) (v_1)^2 ………………..(2)

putting value of v_1 from equation (1) in equation (2)

$m_1 (u_1)^2 = (m_1 + m_2) ({{m_1 u_1} / (m_1 - m_2)})^2$

(m_1 - m_2)^2 = (m_1 + m_2) * m_1

${m_1}^2 + {m_2}^2 - {2m_1 m_2} = {m_1}^2 + m_1m_2$

${m_2}^2 - {2m_1 m_2} = + m_1m_2$

${m_2}^2 = 3{m_1 m_2}$

${m_1}/{m_2} = 1/3$

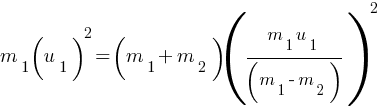
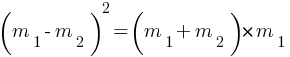
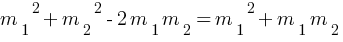
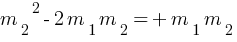
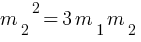
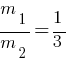
Collisions

Collisions are fascinating events that occur when two or more objects come into contact with each other for a short period of time and apply force to each other, resulting in an exchange of momentum and energy.

In a collision, it may be possible that both bodies do not physically touch each other. for example, collisions between two sub-atomic particles or collisions between two charged particles.

Types of collisions

Elastic Collisions

In an elastic collision, the total kinetic energy and momentum of the system remain conserved. For example, a collision between two billiard balls and a collision between two subatomic particles.

Inelastic Collisions

MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ

हाइड्रोकार्बन

A uniform string of mass M and length 2a is placed symmetrically over a smooth and small pulley … A uniform string of mass M and length 2a is placed symmetrically over a smooth and small pulley … A uniform string of mass M and length 2a is placed symmetrically over a smooth and small pulley … A uniform string of mass M and length 2a is placed symmetrically over a smooth and small pulley … A uniform string of mass M and length 2a is placed symmetrically over a smooth and small pulley …

Share the knowledge spread the love...