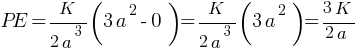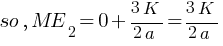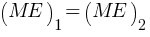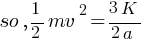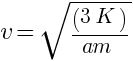A particle of mass approaches a region of force starting from r = +∞. The potential energy function in terms of distance from the origin is given by…
Question :
A particle of mass approaches a region of force starting from r = +∞. The potential energy function in terms of distance from the origin is given by,
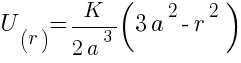 for 0 ≤ r ≤ a
for 0 ≤ r ≤ a
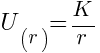 for r ≥ a where K>0 is a positive constant.
for r ≥ a where K>0 is a positive constant.
(a) Derive the force F(r) and determine whether it is repulsive or attractive.
(b) With what velocity should the particle start at r = ∞ to cross over to other side of the origin.
(c) If the velocity of the particle at r = ∞ is 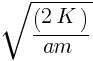 towards the origin describe the motion.
towards the origin describe the motion.
Solution:
(a) F(r) = ? Nature of force whether it is repulsive or attractive =?
Concept: 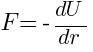
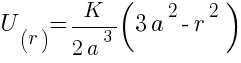
Differentiating above equation wrt dr
For 0 ≤ r ≤ a ![F= - {dU}/{dr} = - {d}/{dr} [{K}/{2a^3}{(3a^2-r^2)}] F= - {dU}/{dr} = - {d}/{dr} [{K}/{2a^3}{(3a^2-r^2)}]](https://mywebpathshala.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_967_1ca5918601aadfba2b2dde3452af06db.png)
![F = - {d}/{dr} [{K}/{2a^3}{(0 - 2r)}] F = - {d}/{dr} [{K}/{2a^3}{(0 - 2r)}]](https://mywebpathshala.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_967_6639d443fe7573fc2161084ec4739d89.png)
![F = [{K r}/{a^3}] F = [{K r}/{a^3}]](https://mywebpathshala.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_967_f8a511571a1ac926ee9e9713124dfdd3.png) F is positive.
F is positive.
For r ≥ a
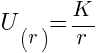
Differentiating above equation wrt dr
![F= - {dU}/{dr} = - {d}/{dr} [{K}/{r}] F= - {dU}/{dr} = - {d}/{dr} [{K}/{r}]](https://mywebpathshala.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_970_6cce83d34d84d72eaaa5f10e738ebee6.png)
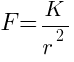 F is positive.
F is positive.
From above it is clear that F is positive in both cases so Force is repulsive in nature.
(b) at r = ∞ v = ? just to cross over to the other side of the origin.
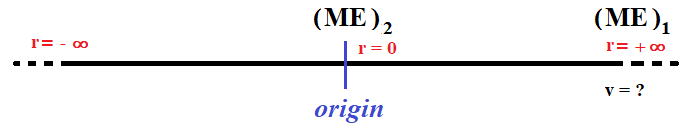
From Law of conservation of energy,
(ME)1 = (ME)2
(ME)1 = KE + PE
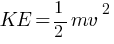
PE =?
For r ≥ a 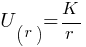
so, at r = ∞ U = 0
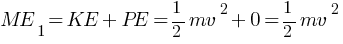
(ME)2 = KE + PE
KE = 0 ( as velocity of particle should be equal to zero, just to pass other side of origin )
At origin PE = ?
For 0 ≤ r ≤ a 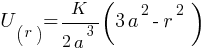
at origin r = 0