A 1.2 kg collar C may slide without friction along a fixed smooth horizontal rod. It is attached to three springs each of constant K= 400 N/m and 150 mm un-deformed length. Knowing that, the collar is released from rest in the position shown in the figure. Determine the maximum velocity it will reach in its motion. Here A, O and B are fixed points.
Question 1:
A 1.2 kg collar C may slide without friction along a fixed smooth horizontal rod. It is attached to three springs each of constant K= 400 N/m and 150 mm un-deformed length. Knowing that, the collar is released from rest in the position shown in the figure. Determine the maximum velocity it will reach in its motion. Here A, O and B are fixed points.
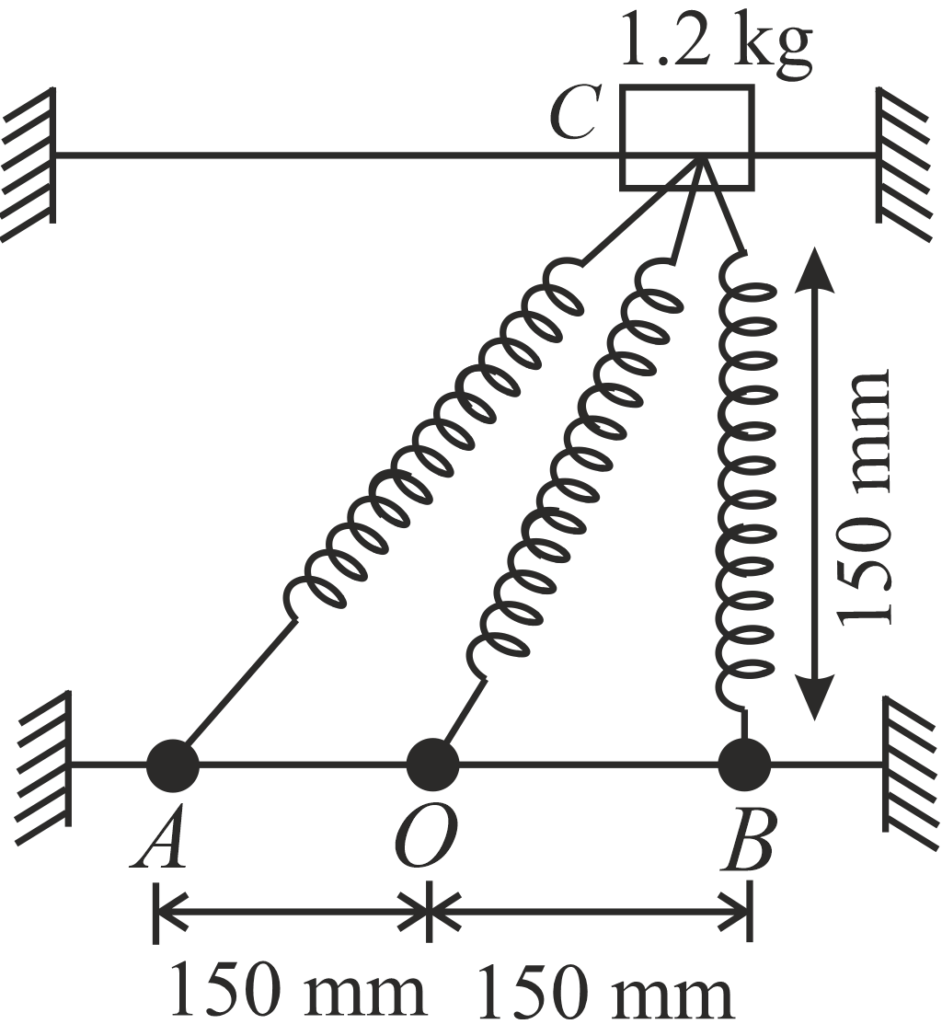
Solution:
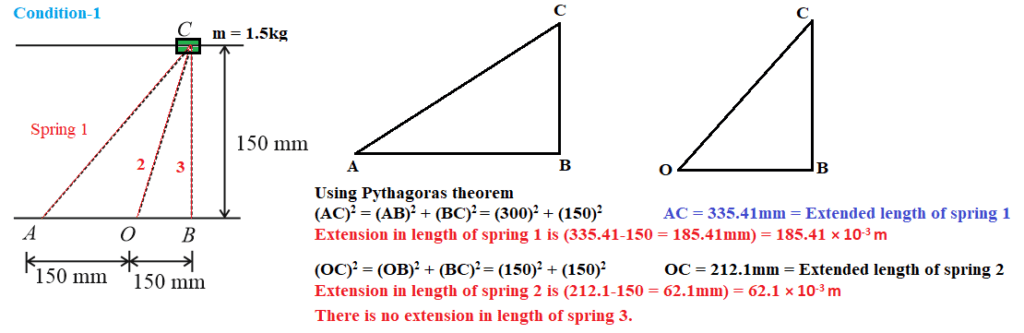
When system is released, collar having mass m = 1.5kg will move to left side as shown in figure condition-1, due to PE of springs 1, 2 and 3. Kinetic energy and hence velocity of mass ‘m’ will be maximum when potential energy of springs is minimum (Law of conservation of energy).
Expression for Potential energy stored in spring 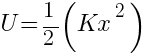
where, x = extension in length of spring K = Spring constant of spring = 400 N/m
Initial potential energy of system (PE)i = PE of spring 1 + PE of spring 2 + PE of spring 3
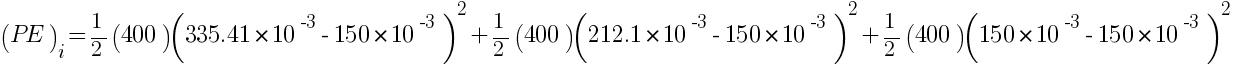
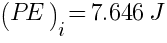
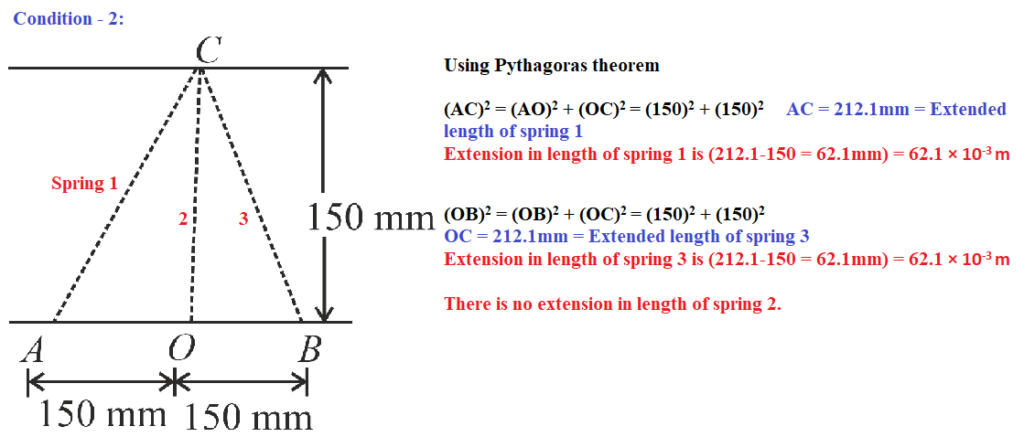
When spring move to left side, a state comes when PE becomes minimum and KE maximum. In this condition ‘ condition-2 ‘ force applied by spring 1 and 3 cancel to each other.
Initial potential energy of system (PE)f = PE of spring 1 + PE of spring 2 + PE of spring 3
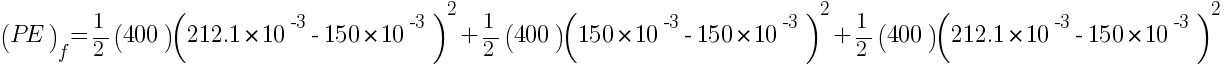
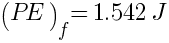
Change in PE = 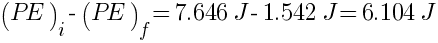
From energy conservation, Change in KE = Change in PE
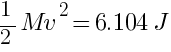 given mass M = 1.5kg
given mass M = 1.5kg
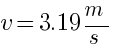
Table of Contents
Question 2:
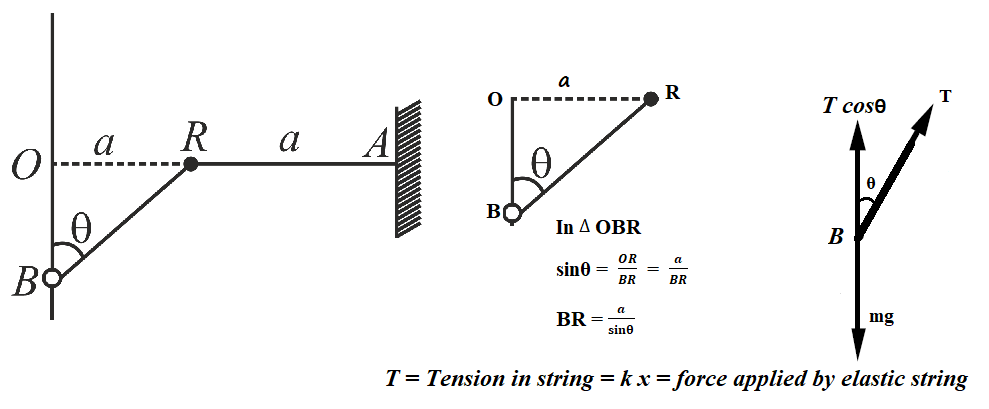
A small bead of mass m is free to slide on a fixed smooth vertical wire, as indicated in the diagram. One end of a light elastic string, of unstretched length a and force constant 2mg/a is attached to B. The string passes through a smooth fixed ring R and the other end of the string is attached to the fixed point A, AR being horizontal. The point O on the wire is at same horizontal level as R, and AR = RO = a.
(i) In the equilibrium position, find OB.(ii) The bead B is raised to a point C of the wire above O, where OC = a, and is released from rest. Find the speed of the bead as it passes O, and find the greatest depth below O of the bead in the subsequent motion.
Force constant of string 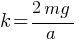
Unstretched / Actual length of string = a
Extended length of string = (BR + RA) = (BR + a) (see diagram)
Extension in length of string 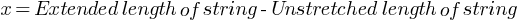
Extension in length of string 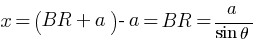
At equilibrium, 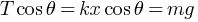
putting value of k and x in above equation,
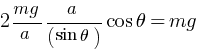
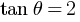
In Δ OBR,
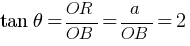
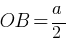
(ii) Bead is raised to point C and released velocity v = ? when it reaches to point O
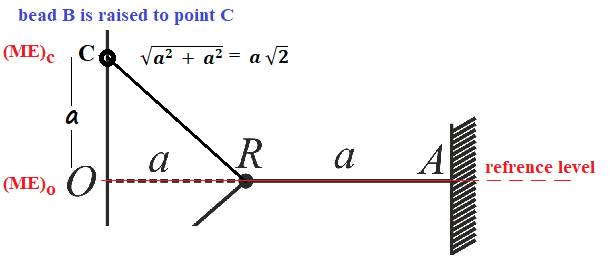
at point C, bead have elastic potential energy (EPE) as well as gravitational potential energy (GPE).
(GPE)c = mg × a = mga
Unstretched / actual length of string = a
Extended length of string 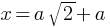
Extension in length of string 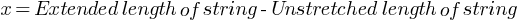
Extension in length of string 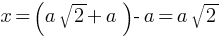
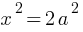
so, Elastic potential energy at point C is 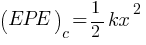
putting value of k and x
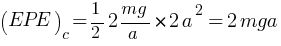
So, total potential energy at point C is,
(PE)c = (EPE)c + (GPE)c = 2mga + mga = 3mga
from law of conservation of energy,
Mechanical energy at C = Mechanical energy at O
(KE)c+(PE)c = (KE)o +(PE)o
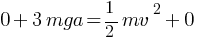
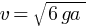 The value of velocity of bead with which bead passes to point O, when released from point C.
The value of velocity of bead with which bead passes to point O, when released from point C.
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ
A 1.2 kg collar C may slide without friction , A 1.2 kg collar C may slide without friction