त्रिभुज कक्षा 5 (Triangle Class 5)
त्रिभुज (Triangle)
- त्रिभुज = त्रि ( तीन ) + भुज ( भुजाएं / बाह )
- वह आकृति जो तीन भुजाओं से घिरी हो उसे त्रिभुज कहते हैं।
- त्रिभुज की तीनों भुजाओं में, किन्ही दो भुजाओं की माप का योग, त्रिभुज की तीसरी भुजा ( या सबसे बड़ी भुजा ) की माप से बड़ा होता है।
- एक त्रिभुज में 3 शीर्ष (3 Vertex), 3 भुजाएं (3 Sides) तथा 3 अंतः कोण (3 Interior Angles) होते है।
Table of Contents
त्रिभुज के कोण
- त्रिभुज में तीन अंतः कोण होते हैं और तीनों अंतः कोणों का योग 180 अंश होता है, जो कि दो समकोण (2 × 90˚) के योग के बराबर है। त्रिभुज के अंदर के कोण को अंतः कोण कहते है।
- ∠ ABC + ∠ BCA + ∠ BAC = 180˚
- त्रिभुज का बाह्य कोण = 180˚ – अंतः कोण
- त्रिभुज का बाह्य कोण = ∠ ABC + ∠ BAC
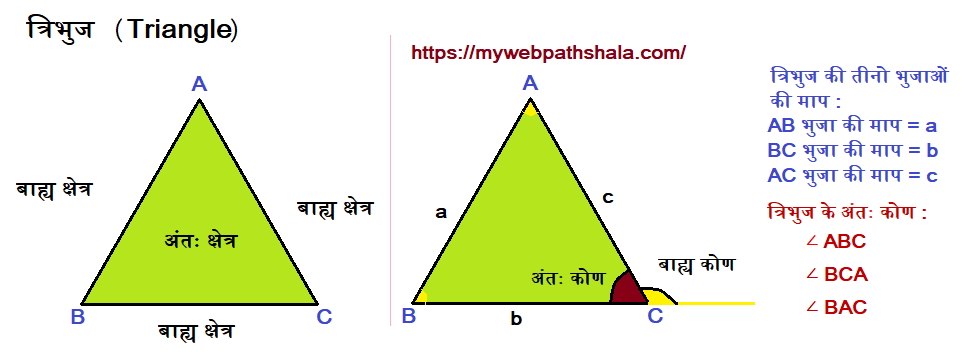
चित्र में दी गई आकृति एक त्रिभुज है, इसे हम 🔺ABC के नाम से प्रदर्शित कर सकते हैं। त्रिभुज के अंदर के भाग को हम अंतः क्षेत्र तथा बाहर के भाग को हम बाह्य क्षेत्र कहते हैं।
त्रिभुज का परिमाप :
- त्रिभुज की तीनो भुजाओं के माप के योग को त्रिभुज का परिमाप कहते हैं।
- त्रिभुज का परिमाप = AB भुजा की माप + BC भुजा की माप + AC भुजा की माप
- त्रिभुज का परिमाप = a + b + c
त्रिभुज के प्रकार (Types of Triangles)
त्रिभुज के अंतः कोणों की माप के आधार पर त्रिभुज के तीन प्रकार होते है।
- समकोण त्रिभुज ( Right Angled Triangle): त्रिभुज के तीनों अंतः कोणों की माप में से एक कोण की माप 90⁰ होती है।
- अधिककोण त्रिभुज ( Obtuse Triangle): त्रिभुज के तीनों अंतः कोणों की माप में से एक कोण की माप 90⁰ से अधिक होती है।
- न्यूनकोण त्रिभुज ( Acute Triangle): त्रिभुज के तीनों अंतः कोणों में से प्रत्येक की माप 90⁰ से कम होती है।
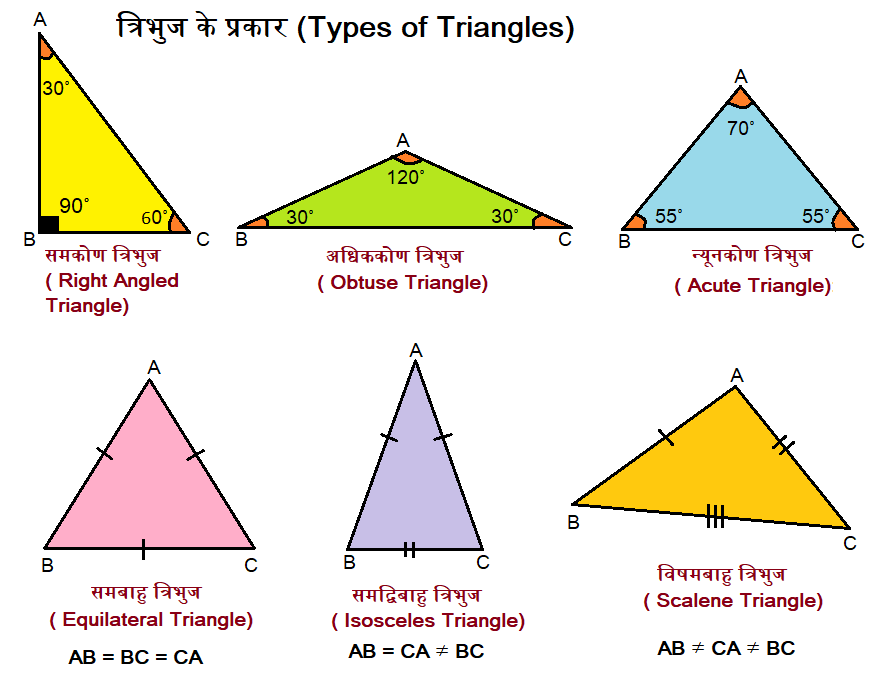
त्रिभुज की भुजाओं की माप के आधार पर भी त्रिभुज के तीन प्रकार होते हैं।
- समबाहु त्रिभुज ( Equilateral Triangle) : समबाहु त्रिभुज की तीनों भुजाओं का माप समान होता है। समबाहु त्रिभुज के तीनों अंतः कोणों में से प्रत्येक की माप 60⁰ होती है।
- समद्विबाहु त्रिभुज ( Isosceles Triangle): समद्विबाहु त्रिभुज की तीनों भुजाओं में से दो भुजाओं की माप बराबर होती है।
- विषमबाहु त्रिभुज ( Scalene Triangle): विषमबाहु त्रिभुज की तीनों भुजाओं की माप अलग अलग होती है।
प्रश्नोत्तर
त्रिभुज क्या होता है? (What is triangle?)
उत्तर: वह आकृति जो तीन भुजाओं से घिरी हो उसे त्रिभुज कहते हैं।
त्रिभुज के अंतः कोणों का योग कितना होता है? (What is sum of Interior Angles of a triangle?)
उत्तर: त्रिभुज के तीनों अंतः कोणों का योग 180 अंश होता है।
समकोण त्रिभुज क्या होता है? (What is right angled triangle?)
उत्तर: समकोण त्रिभुज वह त्रिभुज होता है जिसमें त्रिभुज के तीनों अंतः कोणों की माप में से एक कोण की माप 90⁰ होती है।
विषमकोण त्रिभुज क्या होता है?
उत्तर: विषमकोण त्रिभुज वह त्रिभुज होता है जिसमें त्रिभुज के सभी कोण अलग-अलग होते हैं।
अभ्यास कार्य (पाठ्य पुस्तक से)
प्रश्न 1: निम्नलिखित चित्रों में न्यूनकोण, समकोण तथा अधिककोण त्रिभुज पहचानिए –

हल: न्यूनकोण त्रिभुज – चित्र 1, 3 और 4
समकोण त्रिभुज – केवल चित्र 2
अधिककोण त्रिभुज – केवल चित्र 5
प्रश्न 2: निम्मलिखित त्रिभुजों में ∠ अ ब स की माप बताइये –

हल: ∠ अ ब स की माप = ?
(क) ∵ त्रिभुज के तीनों अंतः कोणों का योग 180° होता है। ∠स अ ब + ∠ अ ब स + ∠ ब स अ = 180°
∠ अ ब स = 180° – ( ∠स अ ब + ∠ ब स अ) = 180° – (50° + 60°) = 180° – 110°= 70°
(ख) ∵ त्रिभुज के तीनों कोणों का योग 180° होता है। ∠स अ ब + ∠ अ ब स + ∠ ब स अ = 180° ∠ अ ब स = 180° – ( ∠स अ ब + ∠ ब स अ) = 180° – (40° + 30°) = 180° – 70°= 110°
(ग) ∵ त्रिभुज के तीनों कोणों का योग 180° होता है। ∠स अ ब + ∠ अ ब स + ∠ ब स अ = 180° ∠ अ ब स = 180° – ( ∠स अ ब + ∠ ब स अ) = 180° – (90° + 40°) = 180° – 130°= 50°
प्रश्न 3: रिक्त स्थानों की पूर्ति करो –
(क) त्रिभुज में ……….. शीर्ष ………… कोण तथा ………… भुजाएँ होती है।
(ख) त्रिभुज के तीनों कोणों का योगफल ………… होता है।
(ग) त्रिभुज की किन्हीं दो भुजाओं की माप का योग तीसरी भुजा से …..…… होता है।
(घ) त्रिभुज की दो भुजाओं की माप का अंतर तीसरी भुजा से ………… होता है।
हल 3: रिक्त स्थानों की पूर्ति करके –
(क) त्रिभुज में ……3….. शीर्ष ……3…… कोण तथा ……3…… भुजाएँ होती है।
(ख) त्रिभुज के तीनों कोणों का योगफल ……180°…… होता है।
(ग) त्रिभुज की किन्हीं दो भुजाओं की माप का योग तीसरी भुजा से …..अधिक…… होता है।
(घ) त्रिभुज की दो भुजाओं की माप का अंतर तीसरी भुजा से …कम… होता है।
MY YouTube Channel Link : 👉🖱 https://www.youtube.com/channel/UCGpC7nWE0-bBv9I53MM8qjQ